课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2023年成考专升本《高等数学二》每日一练试题01月21日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列函数在区间(0,+∞)内单调减少的是().
- A:y=x
- B:y=ex
- C:y=lnx
- D:y=

答 案:D
解 析:AB两项,函数在R上单调递增;C项,y=lnx在(0,+∞)单调递增.
2、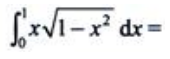 ()
()
答 案:B
解 析: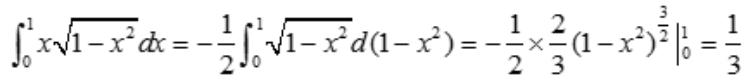
3、设y=f(x)在点x处的切线斜率为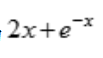 ,则过点(0,1)的曲线方程为()
,则过点(0,1)的曲线方程为()
答 案:A
解 析: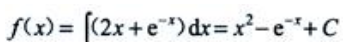 过点(0,1)得C=2,所以
过点(0,1)得C=2,所以
主观题
1、设A,B为两个随机事件,且P(A)=0.8,P(AB)=0.3,求P(A-B).
答 案:解:P(A-B)=P(A-AB)=P(A)-P(AB)=0.8-0.3=0.5.
2、设随机变量ξ的分布列为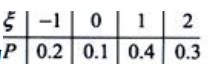 求E(ξ)和D(ξ).
求E(ξ)和D(ξ).
答 案:解:E(ξ)=-1×0.2+0×0.1+1×0.4+2×0.3=0.8.D(ξ)=(-1-0.8)2×0.2+(0-0.8)2×0.1+(1-0.8)2×0.4+(2-0.8)×0.3=1.16.
3、某商店库存100台相同型号的冰箱待售,其中有60台是甲厂生产的,有25台是乙厂生产的,有15台是丙厂生产的.这三个厂生产的冰箱不合格率分别为:0.1,0.4,0.2;一顾客从这批冰箱中随机地买了1台,开机测试后发现是不合格冰箱,由于厂标已脱落,试问这台冰箱最有可能是哪个厂生产的?
答 案:解:设B={顾客买的冰箱不合格),A1={甲厂生产的冰箱),A2=(乙厂生产的冰箱},A3=(丙厂生产的冰箱).由题意,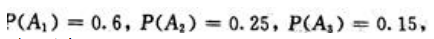 且A1,A2,A3相互独立
且A1,A2,A3相互独立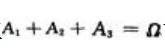 故,由贝叶斯公式得,顾客买不合格的冰箱是甲厂生产的概率为:
故,由贝叶斯公式得,顾客买不合格的冰箱是甲厂生产的概率为: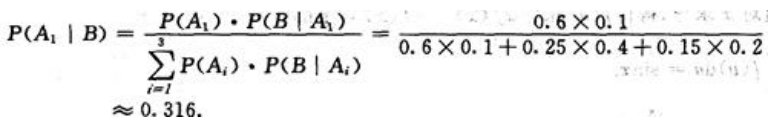
同理,不合格品是乙厂生产的概率为: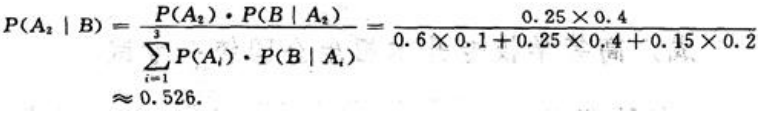
不合格品是丙厂生产的概率为: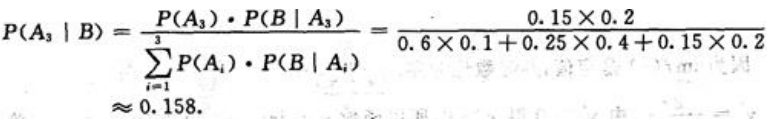
比较上述三个数据知,这台不合格冰箱最有可能是乙厂生产的.
填空题
1、设函数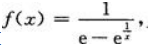 则f(|x+1|)的间断点为()
则f(|x+1|)的间断点为()
答 案:x=1和x=0和x=-2
解 析:由题知,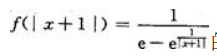 的无定义点为x=1和x=0和x=-2.
的无定义点为x=1和x=0和x=-2.
2、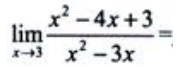 ().
().
答 案: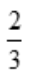
解 析: .
.
3、设函数f(x)在x=2处连续,且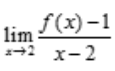 存在,则f(2)=().
存在,则f(2)=().
答 案:1
解 析:因为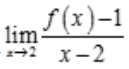 存在,所以
存在,所以 ,即
,即 .因为f(x)在x=2处连续,所以f(2)=1.
.因为f(x)在x=2处连续,所以f(2)=1.
简答题
1、求函数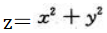 在
在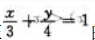 条件下的极值及极值点.
条件下的极值及极值点.
答 案:令 于是
于是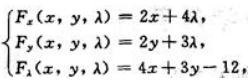 求解方程组
求解方程组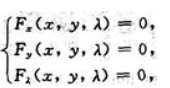 得其驻点
得其驻点 故点
故点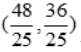 为极值点,且极值为
为极值点,且极值为
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!

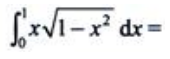 ()
()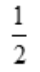
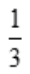
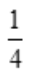
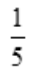
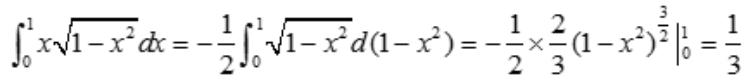
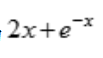 ,则过点(0,1)的曲线方程为()
,则过点(0,1)的曲线方程为()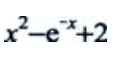
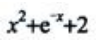
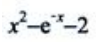
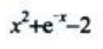
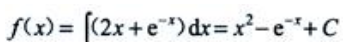 过点(0,1)得C=2,所以
过点(0,1)得C=2,所以
 求E(ξ)和D(ξ).
求E(ξ)和D(ξ).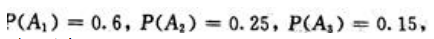 且A1,A2,A3相互独立
且A1,A2,A3相互独立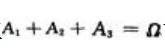 故,由贝叶斯公式得,顾客买不合格的冰箱是甲厂生产的概率为:
故,由贝叶斯公式得,顾客买不合格的冰箱是甲厂生产的概率为: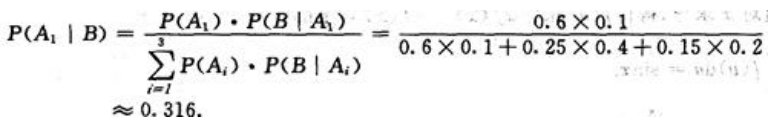
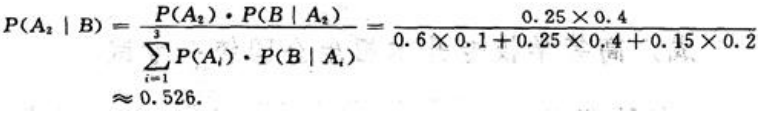
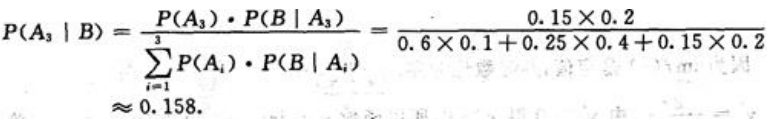
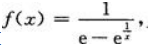 则f(|x+1|)的间断点为()
则f(|x+1|)的间断点为()
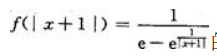 的无定义点为x=1和x=0和x=-2.
的无定义点为x=1和x=0和x=-2.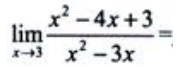 ().
().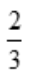
 .
.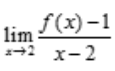 存在,则f(2)=().
存在,则f(2)=().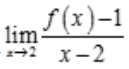 存在,所以
存在,所以 ,即
,即 .因为f(x)在x=2处连续,所以f(2)=1.
.因为f(x)在x=2处连续,所以f(2)=1.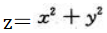 在
在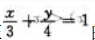 条件下的极值及极值点.
条件下的极值及极值点.
 于是
于是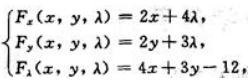 求解方程组
求解方程组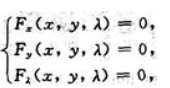 得其驻点
得其驻点 故点
故点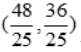 为极值点,且极值为
为极值点,且极值为



