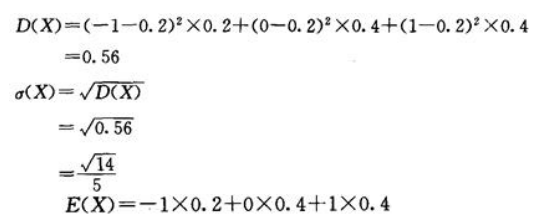2022年成考专升本《高等数学二》每日一练试题12月23日
2022-12-23 10:44:38 来源:吉格考试网
2022年成考专升本《高等数学二》每日一练试题12月23日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数f(x)=1-x3在区间(-∞,+∞)().
- A:单调增加
- B:单调减少
- C:先单调增加,后单调减少
- D:先单调减少,后单调增加
答 案:B
解 析:对任意的x≠0,有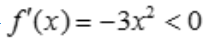 ,仅当x=0时,f(x)的一阶导数为0,故函数在(-∞,+∞)上单调减少.
,仅当x=0时,f(x)的一阶导数为0,故函数在(-∞,+∞)上单调减少.
2、设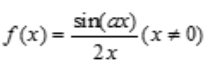 在x=0处连续,且f(0)=
在x=0处连续,且f(0)= ,则a=().
,则a=().
- A:2
- B:-2
- C:-
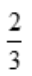
- D:
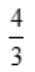
答 案:D
解 析:因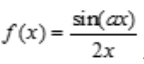 在x=0连续,则
在x=0连续,则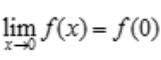 ,
,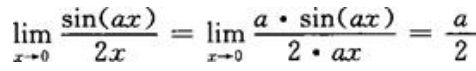 ,又
,又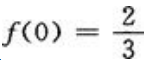 ,所以
,所以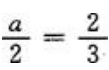 ,即
,即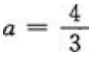 .
.
3、不定积分 等于()
等于()
- A:
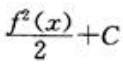
- B:
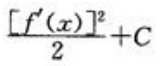
- C:
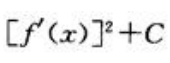
- D:
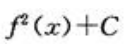
答 案:A
解 析:由分部积分法可知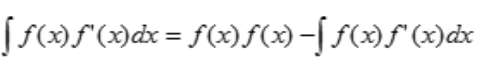 ,所以有
,所以有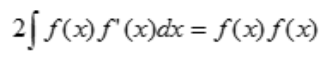 即
即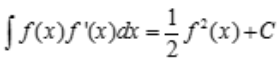 .
.
主观题
1、盒中装着标有数字1、2、3、4的乒乓球各2个,从盒中任意取出3个球,求下列事件的概率:(1)A={取出的3个球上最大的数字是4}.
(2)B={取出的3个球上的数字互不相同}.
答 案:解:基本事件任意取出3个球共有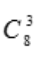 种.(1)取出的3个球上最大的数字是4,有两种可能,即从中取出一个数字为4的球或取出两个数字为4的球,取出一个数字为4的球有
种.(1)取出的3个球上最大的数字是4,有两种可能,即从中取出一个数字为4的球或取出两个数字为4的球,取出一个数字为4的球有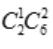 种,取出两个数字为4的球有
种,取出两个数字为4的球有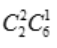 种.事件A中的基本事件为
种.事件A中的基本事件为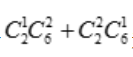 种.所以
种.所以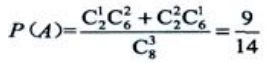 (2)事件B中的基本事件数的计算可以分两步进行:
(2)事件B中的基本事件数的计算可以分两步进行:
先从1,2,3,4的4个数中取出3个数的方法为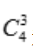 种.
种.
由于每1个数有2个球,再从取出的3个不同数字的球中各取1个球,共有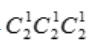 种.
种.
根据乘法原理可知取出的3个球上的数字互不相同的取法共有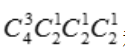 种.
种.
所以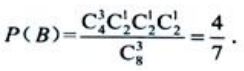
2、某班有党员10人,其中女党员有6人,现选3人组成党支部.设事件A={党支部中至少有1名男党员},求P(A).
答 案:解: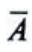 ={党支部中没有男党员},则
={党支部中没有男党员},则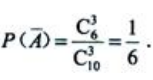 因为
因为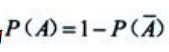 ,所以
,所以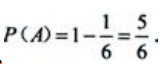
3、甲乙两人独立地向同一目标射击,甲乙两人击中目标的概率分别为0.8与0.5,两人各射击一次,求至少有一人击中目标的概率.
答 案:解:设A={甲击中目标},B={乙击中目标),C={目标被击中)则P(C)=P(A十B)=P(A)+P(B)-P(AB)
=P(A)+P(B)-P(A)P(B)
=0.8+0.5-0.8×0.5
=0.9.
填空题
1、若 则
则 =()
=()
答 案: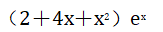
解 析: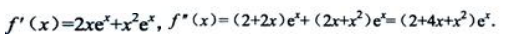
2、 =()
=()
答 案:
解 析:
3、二人独立破译一种密码,他们能独立译出的概率分别为0.3和0.4,则此密码能被破译的概率为().
答 案:0.58
解 析: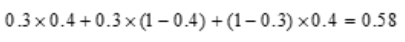 .
.
简答题
1、设随机变量X的概率分布为: 求X的期望、方差以及标准差.
求X的期望、方差以及标准差.
答 案: