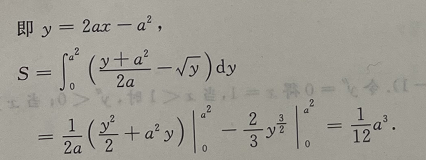2022年成考专升本《高等数学二》每日一练试题12月22日

2022年成考专升本《高等数学二》每日一练试题12月22日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、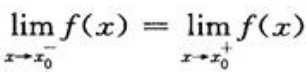是函数f（x）在点x＝x₀处连续的（）.

• A：必要条件
• B：充分条件
• C：充分必要条件
• D：既非充分又非必要条件

答 案：A

解 析：函数f（x）在点x＝x₀处连续的充要条件是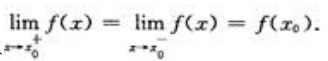因此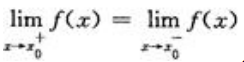只是f（x）在点x₀处连续的必要条件.

2、，则k＝（）.

• A：2
• B：－2
• C：
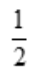
• D：－

答 案：B

解 析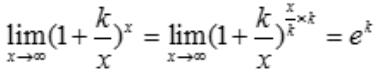：，则k=-2.

3、已知函数f(x)在区间（－∞，＋∞）上单调增加，则使f(x)＞f（2）成立的x的取值范围是（）.

• A：（2，＋∞）
• B：（－∞，0）
• C：（－∞，2）
• D：（0，2）

答 案：A

解 析：因为函数f(x)在区间（－∞，＋∞）上单调增加，故当x＞2时，f(x)＞f（2）.

主观题

1、设f(x)是（-∞，＋∞）内连续的偶函数，证明：．

答 案：证：设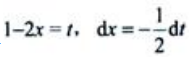，当x＝0时t＝1，x＝1时t＝1．所以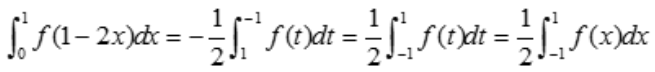又f(x)是（-∞，＋∞）内连续的偶函数，故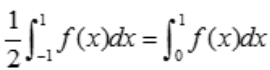，即.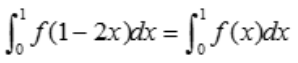

2、设函数y＝ln（x²＋1），求dy．

答 案：解：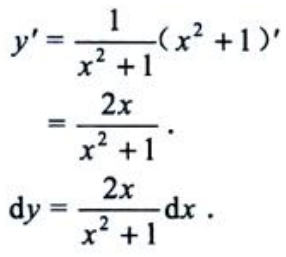

3、盒中装着标有数字1、2、3、4的乒乓球各2个，从盒中任意取出3个球，求下列事件的概率：（1）A＝{取出的3个球上最大的数字是4}．
（2）B＝{取出的3个球上的数字互不相同}．

答 案：解：基本事件任意取出3个球共有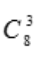种．（1）取出的3个球上最大的数字是4，有两种可能，即从中取出一个数字为4的球或取出两个数字为4的球，取出一个数字为4的球有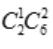种，取出两个数字为4的球有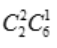种．事件A中的基本事件为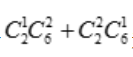种．所以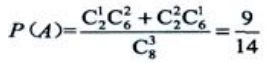（2）事件B中的基本事件数的计算可以分两步进行：
先从1，2，3，4的4个数中取出3个数的方法为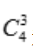种．
由于每1个数有2个球，再从取出的3个不同数字的球中各取1个球，共有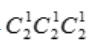种．
根据乘法原理可知取出的3个球上的数字互不相同的取法共有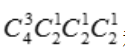种．
所以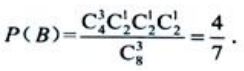

填空题

1、设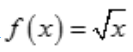，则（）．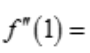

答 案：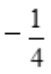

解 析：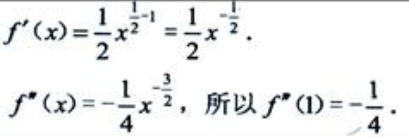

2、已知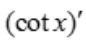＝f(x)，则()．

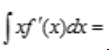答 案：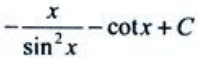

解 析：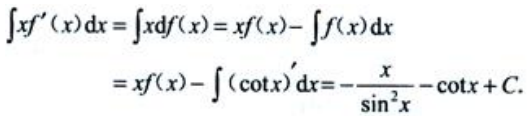

3、设函数y＝ln（1＋x），则y''＝（）．

答 案：

解 析：．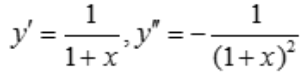

简答题

1、求曲线y=x²与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.

答 案：如图所示，在x=a出切线的斜率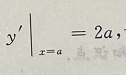为切线方程为