2022年成考专升本《高等数学二》每日一练试题12月17日
2022-12-17 10:46:24 来源:吉格考试网
2022年成考专升本《高等数学二》每日一练试题12月17日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列说法正确的是().
- A:如果A、B是互斥事件,则P(A)+P(B)=1
- B:若P(A)+P(B)=1,则A、B必定是互斥事件
- C:如果A、B是对立事件,则P(A)+P(B)=1
- D:若P(A)+P(B)=1,则事件A与B是对立事件
答 案:C
解 析:AC两项,事件A和B的交集为空集,A与B就是互斥事件,也叫互不相容事件,其中必有一个发生的两个互斥事件叫做对立事件,若A,B是对立事件,则P(A)+P(B)=1;BD两项,互斥事件和对立事件的前提的是A与B事件的交集为空集,虽然P(A)+P(B)=1,但不能保证A与B事件的交集为空集.
2、广义积分 ()
()
- A:
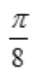
- B:
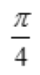
- C:
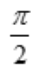
- D:π
答 案:B
解 析: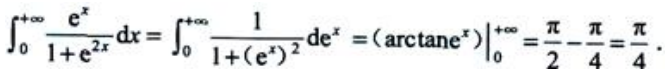
3、设f(x)为连续函数,则 =()
=()
- A:f(2)-f(0)
- B:2[f(2)-f(0)]
- C:

- D:

答 案:C
解 析: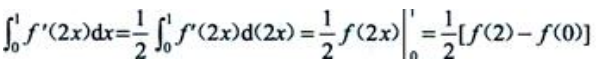
主观题
1、设函数z=z(x,y)由sin(x+y)+ez=0确定,求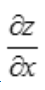 .
.
答 案:解:设F(x,y,z)=sin(x+y)+ez.则 则
则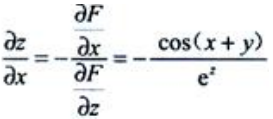
2、设随机变量ξ的分布列为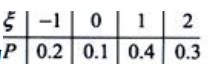 求E(ξ)和D(ξ).
求E(ξ)和D(ξ).
答 案:解:E(ξ)=-1×0.2+0×0.1+1×0.4+2×0.3=0.8.D(ξ)=(-1-0.8)2×0.2+(0-0.8)2×0.1+(1-0.8)2×0.4+(2-0.8)×0.3=1.16.
3、某射手击中10环的概率为0.26,击中9环的概率为0.32,击中8环的概率为0.36,求在一次射击中不低于8环的概率.
答 案:解:设A={击中10环),B={击中9环),C={击中8环),D={击中不低于8环),则D=A+B+C,由于A,B,C相互独立,所以P(D)=P(A+B+C)=P(A)+P(B)+P(C)=0.26+0.32+0.36=0.94
填空题
1、设函数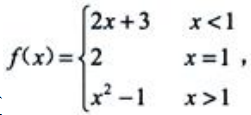 则
则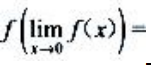 ().
().
答 案:8
解 析: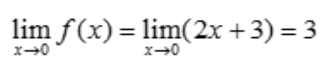 ,故
,故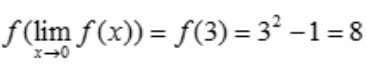 .
.
2、已知函数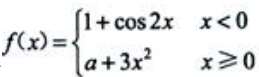 在x=0处连续,则a=().
在x=0处连续,则a=().
答 案:2
解 析:函数f(x)在x=0处连续,可知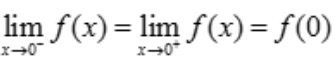 ,
,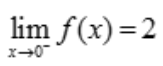 ,
, ,得a=2.
,得a=2.
3、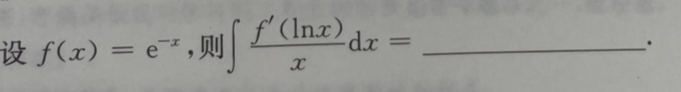
答 案: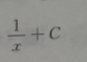
解 析:由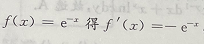 ,所以
,所以 故
故
简答题
1、求由曲线y=x2与x=2,y=0所围成图形分别绕x轴,y轴旋转一周所生成的旋转体体积.
答 案: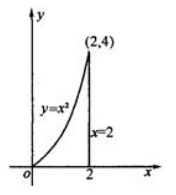
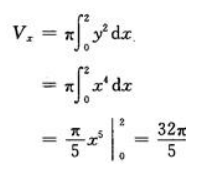 绕y轴旋转一周所得的旋转体体积为
绕y轴旋转一周所得的旋转体体积为