2022年成考专升本《高等数学一》每日一练试题12月10日
2022-12-10 10:41:35 来源:吉格考试网
2022年成考专升本《高等数学一》每日一练试题12月10日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设y=x-2+3,则y'|x=1=()。
- A:3
- B:-3
- C:2
- D:-2
答 案:D
解 析:y'=(x-2+3)'=(x-2)'+3'=-2x-3=-2。
2、函数y=f(x)在点x0处可导的充分必要条件是()。
- A:它在该点处的左导数和右导数存在
- B:它在该点处连续
- C:它在该点处存在极限
- D:它在该点处可微
答 案:D
解 析:D项,对于一元函数来说,函数在某一点可导和在某一点可微等价.A项,函数在某一点的左导数和右导数存在且相等是函数在该点可导的充分必要条件.B项,可导一定连续,但连续不一定可导,例如函数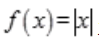 在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
3、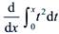 =()。
=()。
- A:x2
- B:2x2
- C:x
- D:2x
答 案:A
解 析:由可变限积分求导公式可知 。
。
主观题
1、设D是由直线y=x与曲线y=x3在第一象限所围成的图形.(1)求D的面积S;
(2)求D绕x轴旋转一周所得旋转体的体积V。
答 案:解:由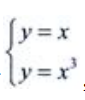 ,知两曲线的交点为(0,0),(1,1)和(-1,-1),则(1)
,知两曲线的交点为(0,0),(1,1)和(-1,-1),则(1)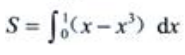

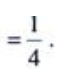 (2)
(2)
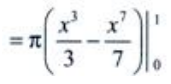
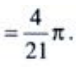
2、设 求C的值。
求C的值。
答 案:解: 则
则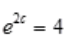 ,有
,有 ,
, 。
。
3、试证:当x>0时,有不等式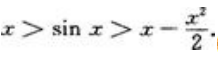
答 案:证:先证x>sinx(x>0)。设f(x)=x-sinx,则f(x)=1-cosx≥0(x>0),所以f(x)为单调递增函数,于是对x>0有f(x)>f(0)=0,即x-sinx>0,亦即x>sinx(x>0)。再证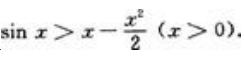
令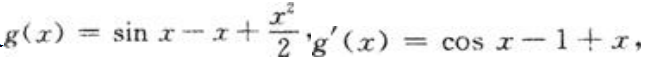
则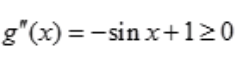 ,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以
,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以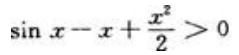 即
即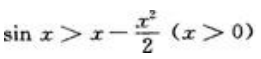
综上可得:当x>0时,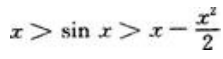 。
。
填空题
1、设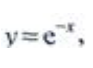 则y''=()。
则y''=()。
答 案:e-x
解 析: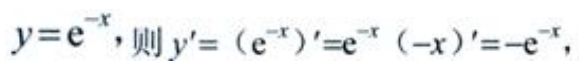
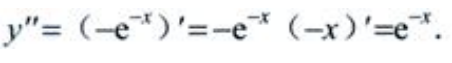
2、函数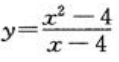 的间断点为()。
的间断点为()。
答 案:x=4
解 析:如果函数f(x)有下列情形之一:(1)在x=x0没有定义;(2)虽在x=x0有定义,但x→x0时limf(x)不存在;(3)虽在x=x0有定义,且x→x0时limf(x)存在,但x→x0时limf(x)≠f(x0),则函数f(x)在点x0为不连续,而点x0称为函数f(x)的间断点.函数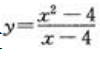 的定义域为x≠4,所以x=4为函数的间断点。
的定义域为x≠4,所以x=4为函数的间断点。
3、函数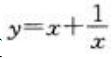 的极大值点的坐标是()。
的极大值点的坐标是()。
答 案:(-1,-2)
解 析: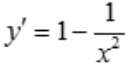 ,令y'=0,得
,令y'=0,得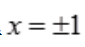 .当x<-1时,y'>0,函数单调增加;当
.当x<-1时,y'>0,函数单调增加;当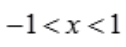 时,y'<0,函数单调减少;当x>1时,y'>0,函数单调增加.故当x=-1时,函数取得极大值为-2,即极大值坐标为(-1,-2)。
时,y'<0,函数单调减少;当x>1时,y'>0,函数单调增加.故当x=-1时,函数取得极大值为-2,即极大值坐标为(-1,-2)。
简答题
1、设sin(t·s)+ln(s—t)=t,求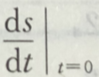 的值.
的值.
答 案:在(t·s)+ln(s—t)=t两边对t求导,视s为t的函数,有 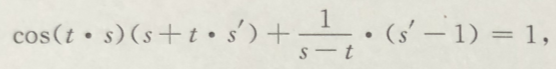 而当t=0时,s=1,代入上式得
而当t=0时,s=1,代入上式得



