课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2025年成考专升本《高等数学一》每日一练试题02月02日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、f(x)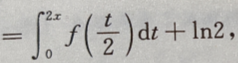 则f(x)=()
则f(x)=()
答 案:B
解 析:因 即
即 此为常系数一阶线性齐次方程,其特征根为r=2,所以其通解为
此为常系数一阶线性齐次方程,其特征根为r=2,所以其通解为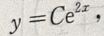 又当x=0时,f(0)=ln2,所以C=ln2,故
又当x=0时,f(0)=ln2,所以C=ln2,故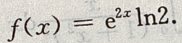
2、函数y=f(x)在点x0处可导的充分必要条件是()。
- A:它在该点处的左导数和右导数存在
- B:它在该点处连续
- C:它在该点处存在极限
- D:它在该点处可微
答 案:D
解 析:D项,对于一元函数来说,函数在某一点可导和在某一点可微等价.A项,函数在某一点的左导数和右导数存在且相等是函数在该点可导的充分必要条件.B项,可导一定连续,但连续不一定可导,例如函数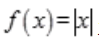 在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
3、下列函数在指定区间上满足罗尔中值定理条件的是()。
- A:
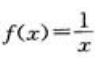 ,x∈[2,0]
,x∈[2,0] - B:f(x)=(x-4)2,x∈[-2,4]
- C:f(x)=sinx,
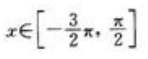
- D:f(x)=|x|,x∈[-1,1]
答 案:C
解 析:罗尔中值定理条件包括:①在闭区间[a,b]上连续;②在开区间(a,b)内可导;③f(a)=f(b).AB两项,条件③均不满足;C项,三个条件均满足;D项,不满足条件②。
主观题
1、试证:当x>0时,有不等式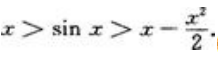
答 案:证:先证x>sinx(x>0)。设f(x)=x-sinx,则f(x)=1-cosx≥0(x>0),所以f(x)为单调递增函数,于是对x>0有f(x)>f(0)=0,即x-sinx>0,亦即x>sinx(x>0)。再证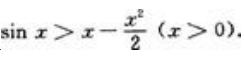
令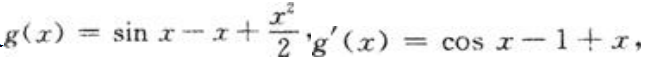
则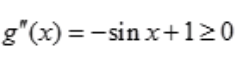 ,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以
,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以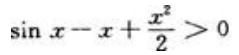 即
即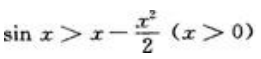
综上可得:当x>0时,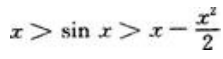 。
。
2、设曲线x=√y、y=2及x=0所围成的平面图形为D.(1)求平面图形D的面积S。
(2)求平面图形D绕y轴旋转一周所生成旋转体的体积Vy。
答 案:解:D的图形见右图阴影部分。 (1)由
(1)由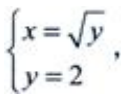 解得
解得 于是
于是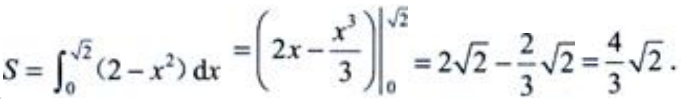
(2)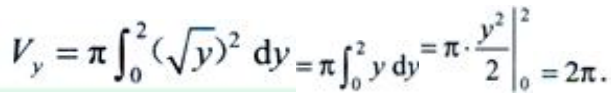
3、计算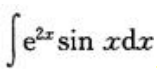 .
.
答 案:解: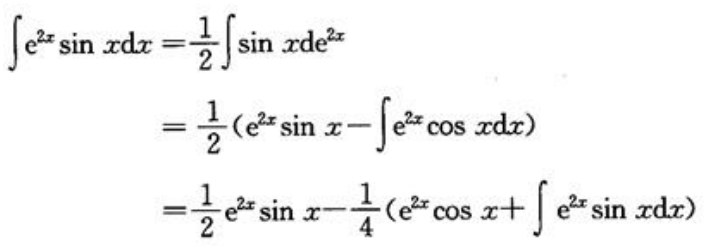 从而有
从而有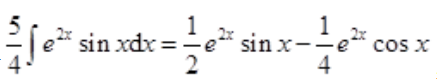 ,所以
,所以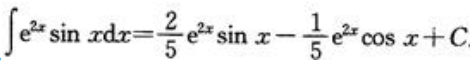
填空题
1、设函数x=3x+y2,则dz=()。
答 案:3dx+2ydy
解 析:
2、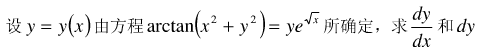
答 案: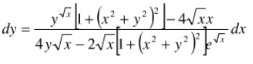
解 析:
3、级数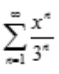 的收敛区间是()。
的收敛区间是()。
答 案:(-3,3)
解 析: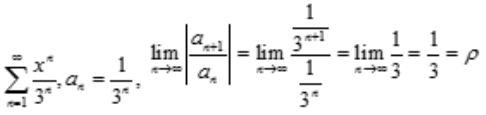 ,因此收敛半径R=
,因此收敛半径R=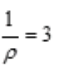 ,收敛区间为(-3,3)。
,收敛区间为(-3,3)。
简答题
1、已知函数f(x)连续,且满足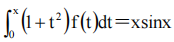 ,求f(x).
,求f(x).
答 案:由于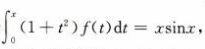 两边同时求导得
两边同时求导得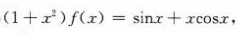 所以
所以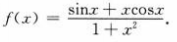
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
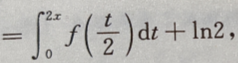 则f(x)=()
则f(x)=()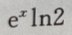

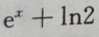
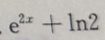
 即
即 此为常系数一阶线性齐次方程,其特征根为r=2,所以其通解为
此为常系数一阶线性齐次方程,其特征根为r=2,所以其通解为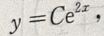 又当x=0时,f(0)=ln2,所以C=ln2,故
又当x=0时,f(0)=ln2,所以C=ln2,故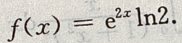
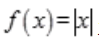 在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。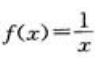 ,x∈[2,0]
,x∈[2,0]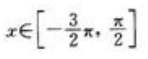
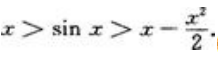
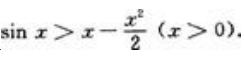
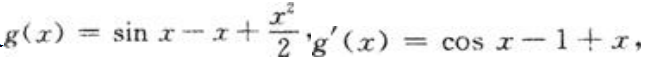
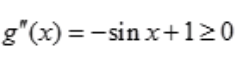 ,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以
,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以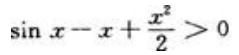 即
即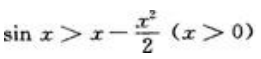
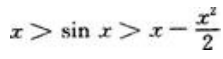 。
。 (1)由
(1)由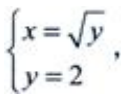 解得
解得 于是
于是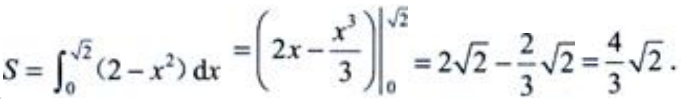
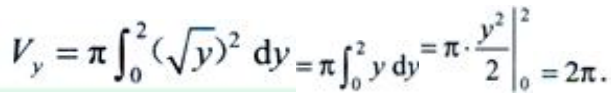
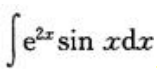 .
.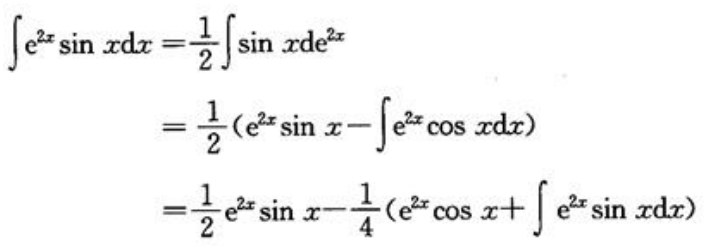 从而有
从而有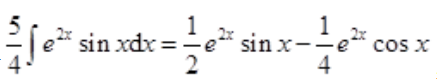 ,所以
,所以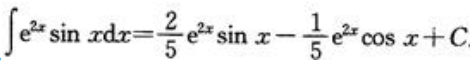

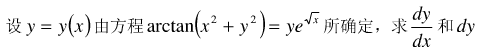
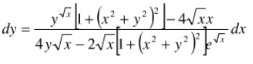

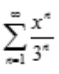 的收敛区间是()。
的收敛区间是()。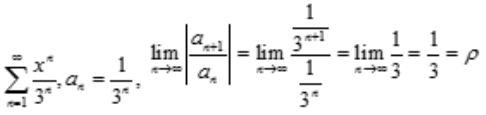 ,因此收敛半径R=
,因此收敛半径R=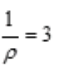 ,收敛区间为(-3,3)。
,收敛区间为(-3,3)。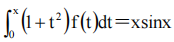 ,求f(x).
,求f(x).
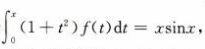 两边同时求导得
两边同时求导得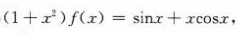 所以
所以