2024年成考专升本《高等数学一》每日一练试题12月21日

2024年成考专升本《高等数学一》每日一练试题12月21日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、在空间直角坐标系中，方程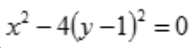表示（）。

• A：两个平面
• B：双曲柱面
• C：椭圆柱面
• D：圆柱面

答 案：A

解 析：由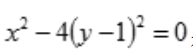得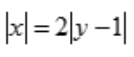，故为两个平面。

2、下列方程为一阶线性微分方程的是（）。  

• A：
• B：
• C：
• D：

答 案：C

解 析：一阶线性微分方程的特点是方程中所含未知函数及其一阶导数都为一次的。因此选C。

3、如果级数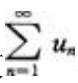收敛，那么以下级数收敛的是（）。

• A：
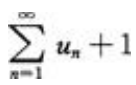
• B：
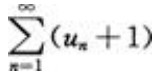
• C：
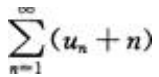
• D：

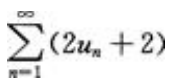
答 案：A

解 析：A项。级数收敛，则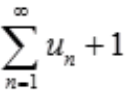收敛；由极限收敛的必要条件可知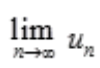，＝0，则B项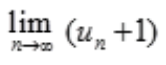，＝1；C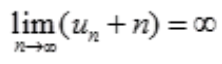项，；D项，。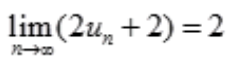

主观题

1、已知直线，平面，试确定m，n的值，使得直线L在平面π上。

答 案：解：此题的关键是抓住直线L在平面π上，即：直线L与平面π平行；直线L上的点也满足平面π的方程，可由下面方法求得m，n的值，要使直线L在平面π上，只要直线L平行于平面π，且有一点在平面π上即可。直线L的方向向量为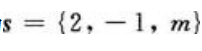，平面π的法线向量为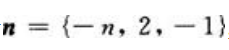，由直线平行于平面π得S·n=0即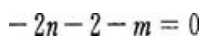①又点P（1，－2，－1）为直线L上的点，把此点的坐标代入平面π的方程得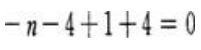②，联立①，②解得：m＝－4n＝1。

2、计算二重积分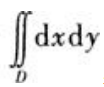，其中D是由曲线y＝1－x²与y＝x²－1所围成．

答 案：解：积分区域D如图所示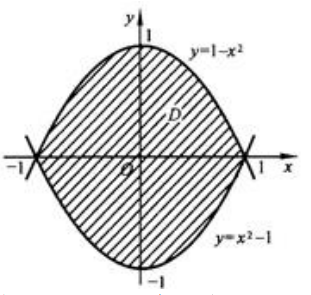。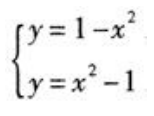解得两组解，对应两个交点（－1，0），（1，0）。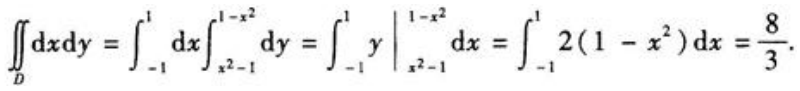

3、某厂要生产容积为V₀的圆柱形罐头盒，问怎样设计才能使所用材料最省?

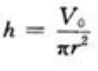答 案：解：设圆柱形罐头盒的底圆半径为r，高为h，表面积为S，则由②得,代入①得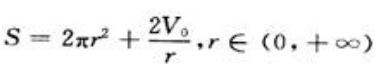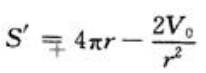现在的问题归结为求r在（0，＋∞）上取何值时，函数S在其上的值最小。
令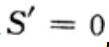,得
由②，当时，相应的h为：。
可见当所做罐头盒的高与底圆直径相等时，所用材料最省。

填空题

1、设z=e^xy，则dz=（）  

答 案：e^xy(ydx+xdy)

解 析：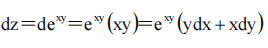

2、设f(x)=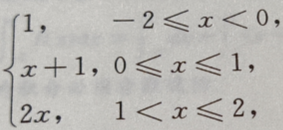则（）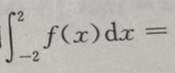

答 案：

解 析：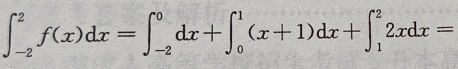

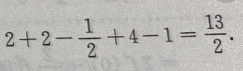
3、幂级数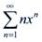的收敛半径R＝（）。

答 案：1

解 析：对于级数，，。

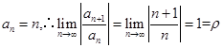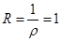简答题

1、求微分方程y”-y’-2y=3e^x的通解。  

答 案：  

解 析：本题考查的知识点为求解二阶线性常系数非齐次微分方程。