2024年成考专升本《高等数学一》每日一练试题12月17日
2024-12-17 11:31:55 来源：吉格考试网
2024年成考专升本《高等数学一》每日一练试题12月17日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、下列等式成立的是（）
- A：
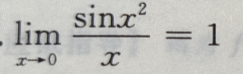
- B：
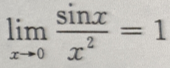
- C：
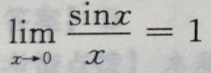
- D：
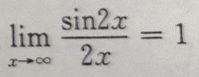
答 案：C
解 析：由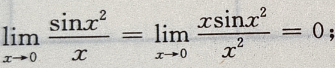
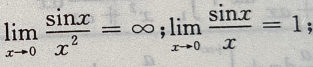
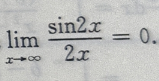
2、设y1、y2是二阶常系数线性齐次方程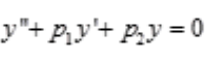
的两个特解，C1、C2为两个任意常数，则下列命题中正确的是（）。
- A：
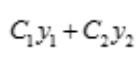为该方程的通解 - B：
不可能是该方程的通解 - C：
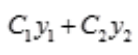为该方程的解 - D：
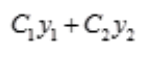不是该方程的解
答 案：C
解 析：由线性方程解的结构定理知
为该方程的解，题中没说明y1、y2是否线性无关，无法判断
是否为通解。
3、设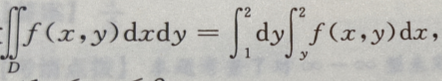
则积分区域D可以表示为（）
- A：
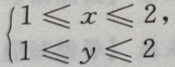
- B：
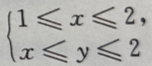
- C：
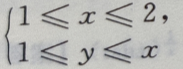
- D：
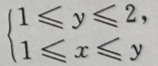
答 案：C
解 析：据右端的二次积分可得积分区域D为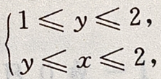
选项中显然没有这个结果，于是须将该区域D用另一种不等式(X-型)表示，故D又可表示为
主观题
1、试证：当x＞0时，有不等式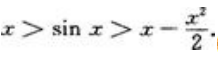
答 案：证：先证x＞sinx（x＞0）。设f（x）＝x－sinx，则f（x）＝1－cosx≥0（x＞0），所以f（x）为单调递增函数，于是对x＞0有f（x）＞f（0）＝0，即x－sinx＞0，亦即x＞sinx（x＞0）。再证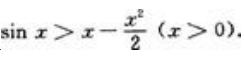
令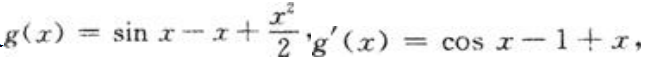
则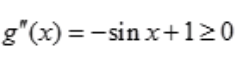
，所以g'(x)单调递增，又g'(x)＝0，可知g'(x)＞g'(0)＝0（x＞0），那么有g（x）单调递增，又g（0）＝0，可知g（x）＞g（0）＝0（x＞0），所以
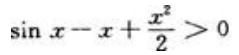即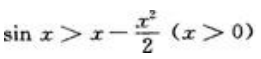
综上可得：当x＞0时，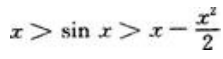
。
2、已知f（π）＝1，且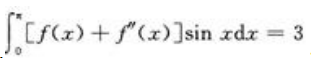
，求f（0）。
答 案：解：
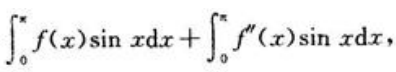对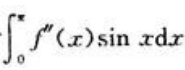
采用凑微分和分部积分后与
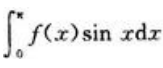相加，代入条件即可求出f（0）。因为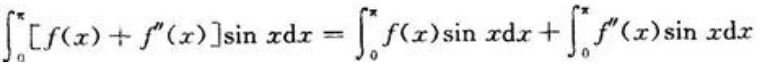
而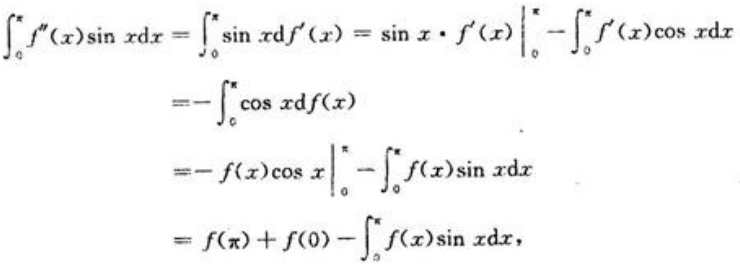
所以
又f（π）＝1，所以f（0）=2。
3、将函数f（x）＝sinx展开为
的幂级数．
答 案：解：由于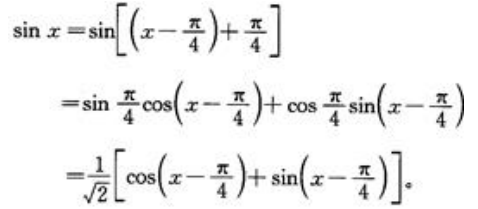
若将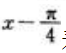
看成整体作为一个新变量，则套用正、余弦函数的展开式可得
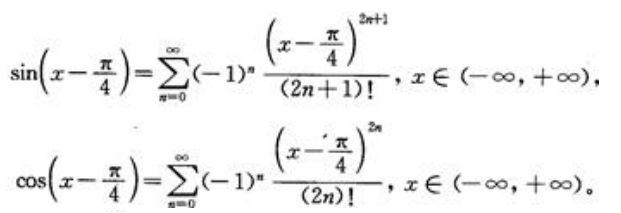从而有
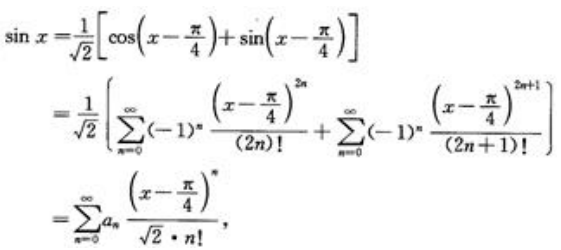其中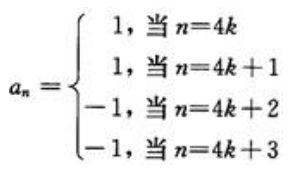
（k为非负整数）。
填空题
1、若二元函数z＝arctan（x2＋y2），则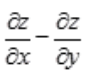
＝（）。
答 案：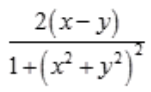
解 析：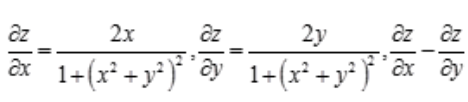
。
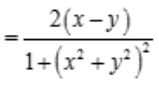2、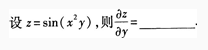
答 案：
解 析：
3、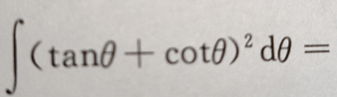
（）
答 案：
解 析：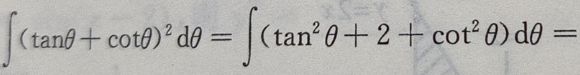
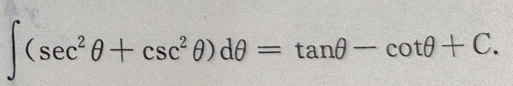
简答题
1、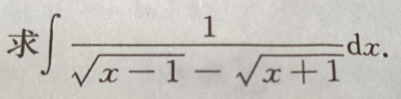
答 案：
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
