2024年成考专升本《高等数学一》每日一练试题11月24日
2024-11-24 11:43:18 来源：吉格考试网
2024年成考专升本《高等数学一》每日一练试题11月24日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、若幂级数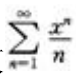
的收敛区间是[1，1)，则级数
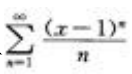的收敛区间是（）。
- A：[-1，1]
- B：[-1，1)
- C：(0，2]
- D：[0，2)
答 案：D
解 析：因为幂级数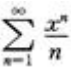
的收敛区间是[-1，1)，则级数
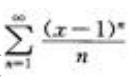的收敛区间为
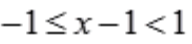，即
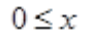＜2。
2、设f（x）为可导函数，则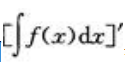
等于（）。
- A：f（x）
- B：f（x）＋C
- C：
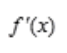
- D：
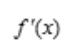＋C
答 案：A
解 析：先积分后求导，积分出来的C求导后就没有了，不改变函数.若先求导后积分,这时候会产生一个常数C，这里的常数不一定是当时的那个常数。
3、设y＝e2x，则dy＝（）。
- A：e2xdx
- B：2e2xdx
- C：
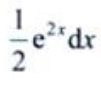
- D：－2e2xdx
答 案：B
解 析：由复合函数的求导法则可知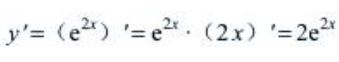
，故
。
主观题
1、将f（x）＝arctanx（|x|＜1）展开成x的幂级数。
答 案：解：因为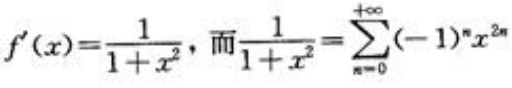
，两边积分可得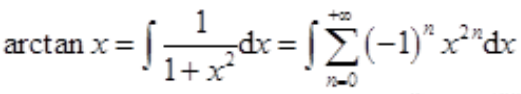
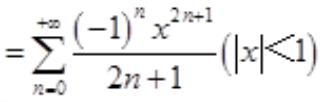
2、设
求C的值。
答 案：解：
则
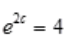，有
，
。
3、某厂要生产容积为V0的圆柱形罐头盒，问怎样设计才能使所用材料最省?
答 案：解：设圆柱形罐头盒的底圆半径为r，高为h，表面积为S，则
由②得
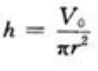,代入①得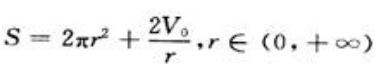
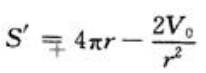现在的问题归结为求r在（0，＋∞）上取何值时，函数S在其上的值最小。
令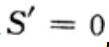
,得
由②，当
时，相应的h为：
。
可见当所做罐头盒的高与底圆直径相等时，所用材料最省。
填空题
1、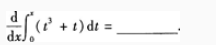
答 案：x3+x
解 析：
2、函数F(x)=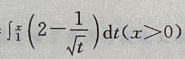
的单调递减区间是（）
答 案：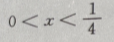
解 析：由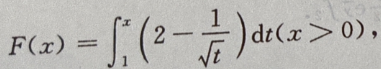
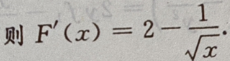
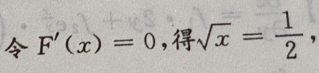
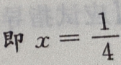故
F(x)单调递减。
3、设f（x）＝3x，g（x）＝x3，则
＝（）。
答 案：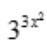
·1n3
解 析：g（x）＝x3，g'（x）＝3x2，则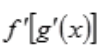
＝f'（3x2），注意等号右端的含义为f（
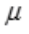）在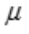
＝3x2处的导数，而f（x）＝3x，即f（）＝
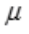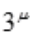，则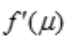
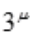＝ln3，所以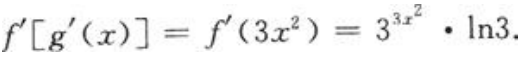
简答题
1、
答 案：积分区域D如图2-1所示。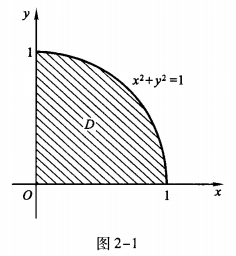 
解法1利用极坐标系。
解 析：本题考查的知识点为计算二重积分；选择积分次序或利用极坐标计算。 
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
