2024年成考专升本《高等数学二》每日一练试题09月16日-吉格考试网

2024年成考专升本《高等数学二》每日一练试题09月16日

2024-09-16 11:35:54 来源：吉格考试网

课程题库

分享到空间 分享到新浪微博 分享到QQ 分享到微信

2024年成考专升本《高等数学二》每日一练试题09月16日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）

答案：错

解析：所以

单选题

1、设则＝（）.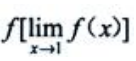

A：0
B：-1
C：-3
D：-5

答案：C

解析：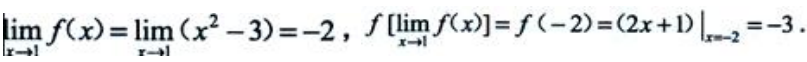

2、设y^（n-2）=x^²＋sinx，则y^（n）=（）

A：2-sinx
B：2-cosx
C：2＋sinx
D：2＋cosx

答案：A

解析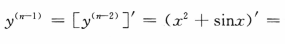：2x+cosx，所以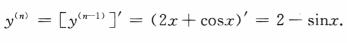

主观题

1、某班有党员10人，其中女党员有6人，现选3人组成党支部．设事件A＝{党支部中至少有1名男党员}，求P（A）．

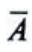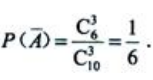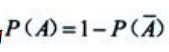答案：解：＝{党支部中没有男党员}，则因为，所以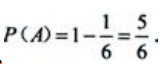

2、某商店库存100台相同型号的冰箱待售，其中有60台是甲厂生产的，有25台是乙厂生产的，有15台是丙厂生产的．这三个厂生产的冰箱不合格率分别为：0.1，0.4，0.2；一顾客从这批冰箱中随机地买了1台，开机测试后发现是不合格冰箱，由于厂标已脱落，试问这台冰箱最有可能是哪个厂生产的？

答案：解：设B＝{顾客买的冰箱不合格），A₁＝{甲厂生产的冰箱），A₂＝（乙厂生产的冰箱}，A₃＝（丙厂生产的冰箱）．由题意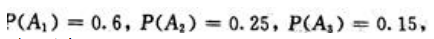，且A₁，A₂，A₃相互独立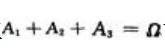故，由贝叶斯公式得，顾客买不合格的冰箱是甲厂生产的概率为：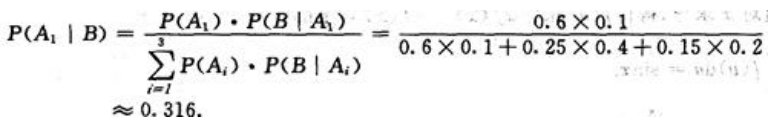
同理，不合格品是乙厂生产的概率为：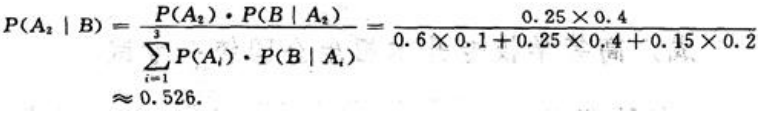
不合格品是丙厂生产的概率为：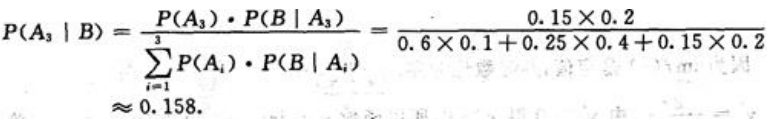
比较上述三个数据知，这台不合格冰箱最有可能是乙厂生产的．

填空题

1、（）．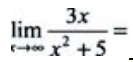

答案：

解析：由洛必达法则有．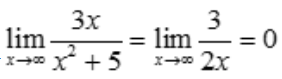

2、已知f（x）的一个原函数为2lnx,则()．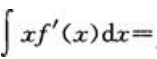

答案：

解析：由分部积分法可知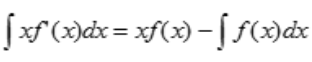，由题可知f（x）的一个原函数为2lnx，所以，故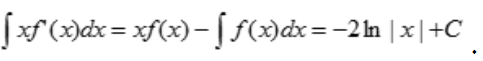

简答题

1、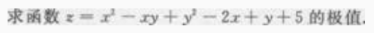

答案：

2、甲、乙二人单独译出某密码的概率分别为0.6和0.8，求此密码被破译的概率。

答案：本题考查的知识点是事件相互独立的概念和概率的加法公式。

温馨提示：因考试政策、内容不断变化与调整，本站提供的以上信息仅供参考，如有异议，请考生以权威部门公布的内容为准！

感谢您信任并使用聚题库系统。我们深知个人信息和隐私保护的重要性，为了更好地保护您的个人权益，在使用产品前请充分阅读并理解《用户服务协议》和《隐私协议》。

长沙聚优教育咨询有限公司（以下简称“长沙聚优”）在此特别提醒您在使用相关服务前，请认真阅读协议条款内容，确保您充分理解协议中各条款，特别是免除或者限制责任、法律适用和管辖的条款，以及开通或使用某项服务的单独协议，并选择接受或不接受。如你未满18周岁，请在法定监护人陪同下仔细阅读并充分理解本协议，并征得法定监护人的同意后使用“聚题库”软件及相关服务。除非您接受本协议所有条款，否则您无权注册、登录或使用本协议所涉服务。

隐私权政策适用我们提供的软件、网站、服务，包括但不限于适用于电脑、移动智能终端产品及服务。

本隐私权政策旨在帮助您了解我们会收集哪些数据，为什么收集这些数据、会利用这些数据做什么以及我们如何保护这些数据。了解这些内容，对于您行使个人权利及保护您的个人信息至关重要，请您在使用我们产品或服务前务必抽出时间认真阅读本政策。