2024年成考专升本《高等数学一》每日一练试题09月08日

2024年成考专升本《高等数学一》每日一练试题09月08日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、微分方程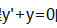的通解为y=（）。  

• A：e-x+C
• B：-e-x+C
• C：Ce^-x
• D：Ce^x

答 案：C

解 析：所给方程为可分离变量方程。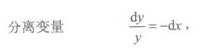  

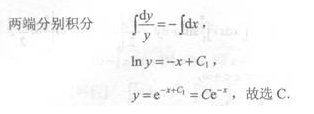
2、设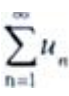与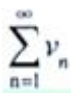都为正项级数，且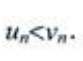则下列结论正确的是（）。

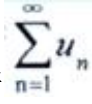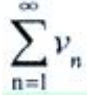• A：若收敛，则收敛
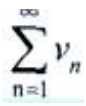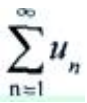• B：若发散，则发散
• C：若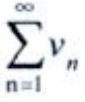收敛，则收敛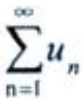
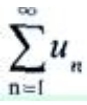• D：若收敛，则发散

答 案：C

解 析：由正项级数的比较判别法可知，若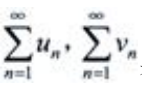都为正项级数，且则当收敛时，可得知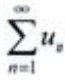必定收敛．

3、设f（x）在点x₀处取得极值，则（）。

• A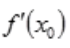：不存在或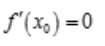
• B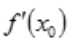：必定不存在
• C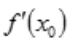：必定存在且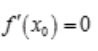
• D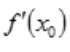：必定存在，不一定为零

答 案：A

解 析：若点x₀为f（x）的极值点，可能为两种情形之一：（1）若f（x）在点x₀处可导，由极值的必要条件可知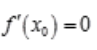；（2）如f（x）＝|x|在点x＝0处取得极小值，但f（x）＝|x|在点x＝0处不可导，这表明在极值点处，函数可能不可导。

主观题

1、欲围造一个面积为15000平方米的运动场，其正面材料造价为每平方米600元，其余三面材料造价为每平方米300元，试问正面长为多少米才能使材料费最少?

答 案：解：设运动场正面围墙长为x米，则宽为，设四面围墙高相同，记为h，则四面围墙所用材料费用，f（x）为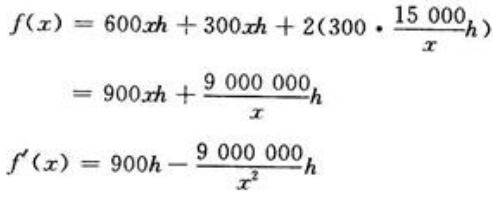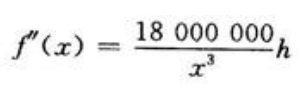令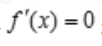得驻点x₁＝100，x₂＝－100（舍掉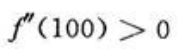），由于驻点唯一，且实际问题中存在最小值，可知x＝100米，侧面长150米时，所用材料费最小。

2、计算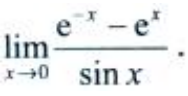

答 案：解：利用洛必达法则，得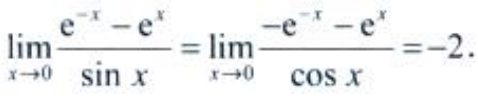

3、求微分方程的通解。

答 案：解：原方程对应的齐次方程为，特征方程及特征根为r²－4r＋4＝0，r_1，2＝2，齐次方程的通解为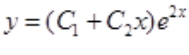。在自由项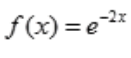中，a=-2不是特征根，所以设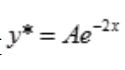，代入原方程，有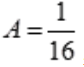，故原方程通解为。

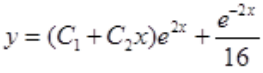填空题

1、微分方程xy'+y＝0满足y（1）＝1的解为y＝（）  

答 案：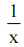

解 析：由xy'+y＝0得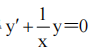，通解为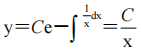，将y（1）＝1代入通解，得C＝1,故所求的解为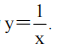

2、广义积分＝（）。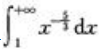

答 案：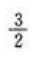

解 析：。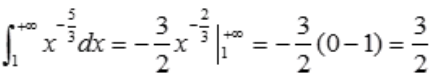

3、设I=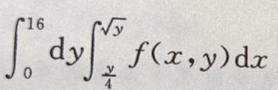交换积分次序，则有I=（）

答 案：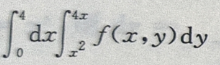

解 析：的积分区域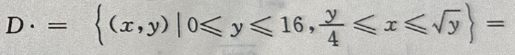

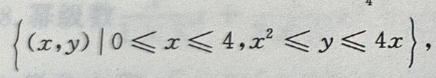
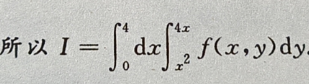
简答题

1、设抛物线Y=1-x²与x轴的交点为A、B，在抛物线与x轴所围成的平面区域内，以线段AB为下底作内接等腰梯形ABCD（如图2—1所示）。设梯形上底CD长为2x，面积为S（x）。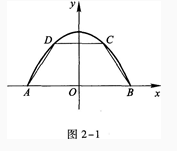
（1）写出S（x）的表达式；
（2）求S（x）的最大值。  

答 案：