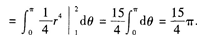2024年成考专升本《高等数学一》每日一练试题08月30日

2024年成考专升本《高等数学一》每日一练试题08月30日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、当x→0时，与3x²＋2x³等价的无穷小量是（）。

• A：2x³
• B：3x²
• C：x²
• D：x³

答 案：B

解 析：由于当x→0时，3x²为x的二阶无穷小量，2x³为x的三阶无穷小量，因此3x²＋2x³为x的二阶无穷小量，即。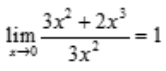

2、曲线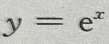与其过原点的切线及y轴所围面积为（）

• A：
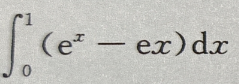
• B：
• C：
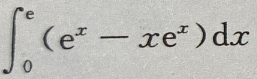
• D：

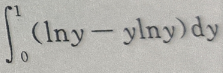
答 案：A

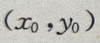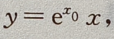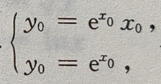解 析：设为切点，则切线方程为联立得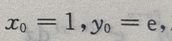所以切线方程为y=ex，故所求面积为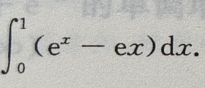

3、微分方程的阶数为（）。

• A：1
• B：2
• C：3
• D：4

答 案：A

解 析：微分方程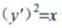所含有未知函数y的导数最高阶数为1，为一阶微分方程。

主观题

1、设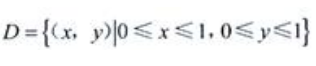，求。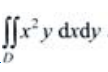

答 案：解：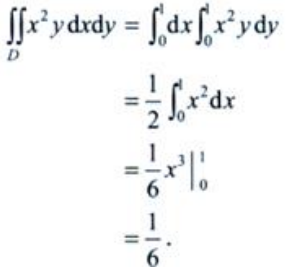

2、试证：当x＞0时，有不等式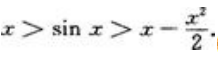

答 案：证：先证x＞sinx（x＞0）。设f（x）＝x－sinx，则f（x）＝1－cosx≥0（x＞0），所以f（x）为单调递增函数，于是对x＞0有f（x）＞f（0）＝0，即x－sinx＞0，亦即x＞sinx（x＞0）。再证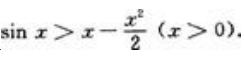
令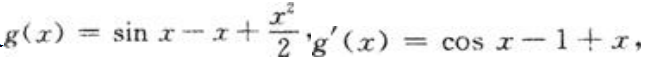
则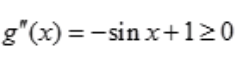，所以g'(x)单调递增，又g'(x)＝0，可知g'(x)＞g'(0)＝0（x＞0），那么有g（x）单调递增，又g（0）＝0，可知g（x）＞g（0）＝0（x＞0），所以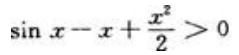即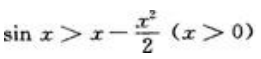
综上可得：当x＞0时，。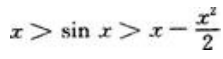

3、求。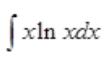

答 案：解：。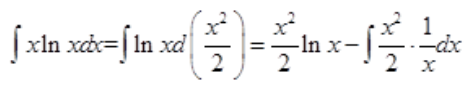

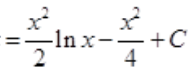填空题

1、  

答 案：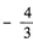

解 析：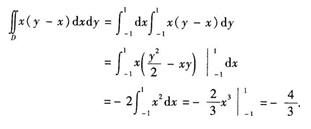

2、设f'(x₀)＝2，f(x₀)＝0，则＝（）。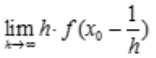

答 案：-2

解 析：。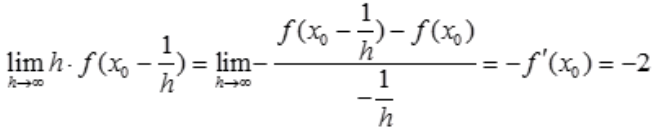

3、过坐标原点且与平面2x-y+z+1=0平行的平面方程为______。  

答 案：2x-y+z=0

解 析：已知平面的法线向量n₁=（2，-1，1），所求平面与已知平面平行，可设所求平面方程为2x-y+z+D=0，将x=0，y=0，z=0代入上式，可得D=0，因此所求平面方程为2x-y+z=0。

简答题

1、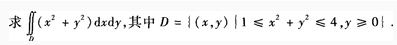  

答 案：积分区域D为半圆环域，利用极坐标计算此二重积分较方便。在极坐标系下，X²+Y²=1可以化为r=1；x²+y²=4可以化为r=2。因此区域D可以表示为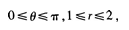因此