2024年成考专升本《高等数学二》每日一练试题08月27日

2024年成考专升本《高等数学二》每日一练试题08月27日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、以下结论正确的是（）.

• A：函数f（x）的导数不存在的点，一定不是f（x）的极值点
• B：若x₀点为函数f（x）的驻点，则x₀必为f（x）的极值点
• C：若函数f（x）在点x₀处取极值，且f'（x）存在，则必有f'（x）＝0
• D：若函数f（x）在点x₀处连续，则f'（x）一定存在

答 案：C

解 析：A项，函数f(x)的极值点不一定是可导点；B项，驻点是导数为零的点，不一定是极值点，比如当f(x)＝x³时，x＝0为其驻点，但不是其极值点；D项，连续不一定可导.

2、下列说法正确的是（）.

• A：如果A、B是互斥事件，则P（A）＋P（B）＝1
• B：若P（A）＋P（B）＝1，则A、B必定是互斥事件
• C：如果A、B是对立事件，则P（A）＋P（B）＝1
• D：若P（A）＋P（B）＝1，则事件A与B是对立事件

答 案：C

解 析：AC两项，事件A和B的交集为空集，A与B就是互斥事件，也叫互不相容事件，其中必有一个发生的两个互斥事件叫做对立事件，若A，B是对立事件，则P（A）＋P（B）＝1；BD两项，互斥事件和对立事件的前提的是A与B事件的交集为空集，虽然P（A）＋P（B）＝1，但不能保证A与B事件的交集为空集.

主观题

1、盒中装着标有数字1、2、3、4的乒乓球各2个，从盒中任意取出3个球，求下列事件的概率：（1）A＝{取出的3个球上最大的数字是4}．
（2）B＝{取出的3个球上的数字互不相同}．

答 案：解：基本事件任意取出3个球共有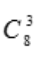种．（1）取出的3个球上最大的数字是4，有两种可能，即从中取出一个数字为4的球或取出两个数字为4的球，取出一个数字为4的球有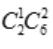种，取出两个数字为4的球有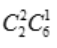种．事件A中的基本事件为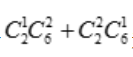种．所以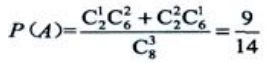（2）事件B中的基本事件数的计算可以分两步进行：
先从1，2，3，4的4个数中取出3个数的方法为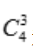种．
由于每1个数有2个球，再从取出的3个不同数字的球中各取1个球，共有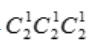种．
根据乘法原理可知取出的3个球上的数字互不相同的取法共有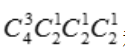种．
所以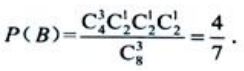

2、计算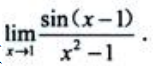

答 案：解：利用重要极限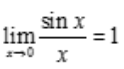，则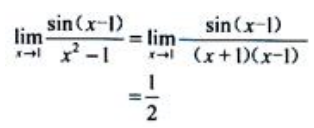

填空题

1、设事件A，B相互独立，且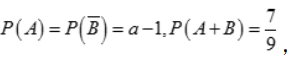则常数a＝（）

答 案：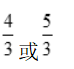

解 析：由加法公式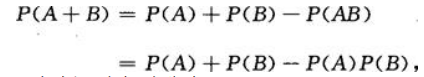  

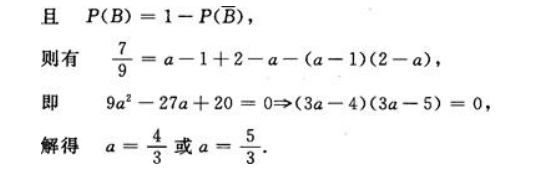
2、＝()．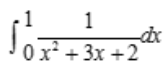

答 案：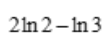

解 析：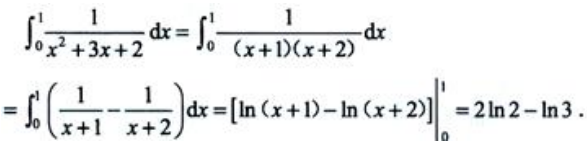

简答题

1、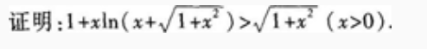  

答 案：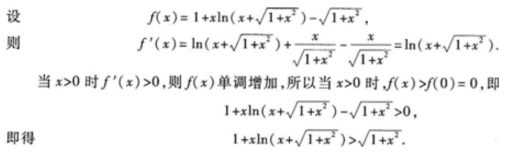

2、计算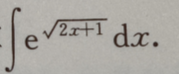

答 案：