2024年成考专升本《高等数学一》每日一练试题07月13日
2024-07-13 11:31:21 来源:吉格考试网
2024年成考专升本《高等数学一》每日一练试题07月13日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、方程2x2+y2+z2=1表示()。
- A:椭球面
- B:一个点
- C:锥面
- D:球面
答 案:A
解 析:因为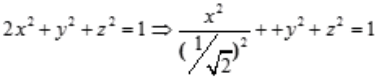 ,故该方程表示的是椭球面。
,故该方程表示的是椭球面。
2、曲线 与其过原点的切线及y轴所围面积为()
与其过原点的切线及y轴所围面积为()
- A:
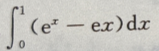
- B:

- C:
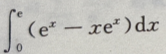
- D:

答 案:A
解 析:设(x0,y0)为切点,则切线方程为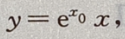 联立
联立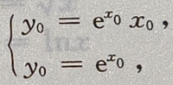 得x0=1,y0=e,所以切线方程为y=ex,故所求面积为
得x0=1,y0=e,所以切线方程为y=ex,故所求面积为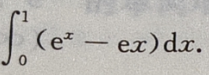
3、 纸笔测验操作方便,是最常用的学业评价方法。在化学教学中运用纸笔测验.重点不宜放在( )。
- A:对化学用语的识别能力
- B:对化学基本原理的理解
- C:对元素化合物知识的认识
- D:对实验操作技能的考查
答 案:D
解 析:对实验操作技能的考查适合采用活动表现评价的方式。故本题选D。
主观题
1、求微分方程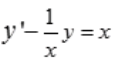 的通解。
的通解。
答 案:解: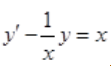 为一阶线性微分方程,则
为一阶线性微分方程,则
2、曲线y2+2xy+3=0上哪点的切线与x轴正向所夹的角为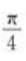 ?
?
答 案:解:将y2+2xy+3=0对x求导,得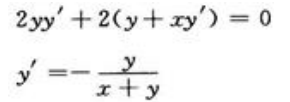 欲使切线与x轴正向所夹的角为
欲使切线与x轴正向所夹的角为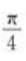 ,只要切线的斜率为1,即
,只要切线的斜率为1,即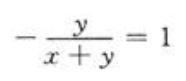 亦即x+2y=0,设切点为(x0,y0),则x0+2y0=0①
亦即x+2y=0,设切点为(x0,y0),则x0+2y0=0①
又切点在曲线上,即y02+2x0y0+3=0②
由①,②得y0=±1,x0=±2
即曲线上点(-2,1),(2,-1)的切线与x轴正向所夹的角为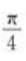 。
。
3、设f(x)是以T为周期的连续函数,a为任意常数,证明: 。
。
答 案:证:因为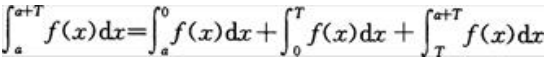 令x=T+t,做变量替换得
令x=T+t,做变量替换得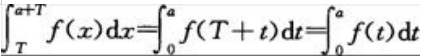 故
故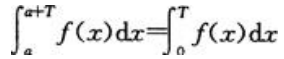
填空题
1、曲线y=2x2在点(1,2)处有切线,曲线的切线方程为y=()。
答 案:4x-2
解 析:点(1,2)在曲线y=2x2上,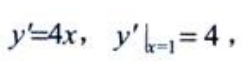 过点(1,2)的切线方程为y-2=4(x-1),y=4x-2。
过点(1,2)的切线方程为y-2=4(x-1),y=4x-2。
2、微分方程y"+2y'+y=0满足初始条件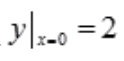 ,
,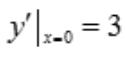 的特解是()。
的特解是()。
答 案:(2+5x)e-x
解 析:微分方程的特征方程为 ,得
,得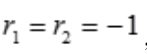 ,微分方程的通解为
,微分方程的通解为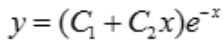 .将
.将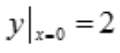 ,
,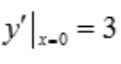 代入得
代入得 ,
,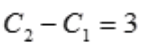 ,则
,则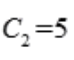 .故微分方程通解为
.故微分方程通解为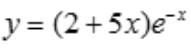 。
。
3、曲线y=x2-x在点(1,0)处的切线斜率为()。
答 案:1
解 析:点(1,0)在曲线y=x2-x上,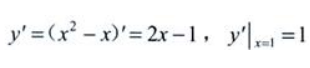 ,故点(1,0)处切线的斜率为1。
,故点(1,0)处切线的斜率为1。
简答题
1、讨论级数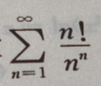 敛散性。
敛散性。
答 案: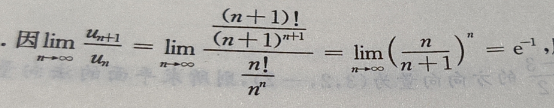 所以级数收敛。
所以级数收敛。



