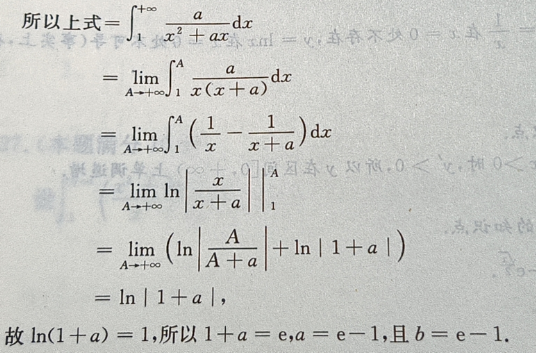课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考专升本《高等数学一》每日一练试题06月24日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、微分方程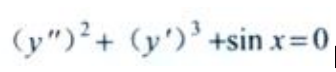 的阶数为()。
的阶数为()。
答 案:B
解 析:所给方程含有未知函数y的最高阶导数是2阶,因此方程的阶数为2。
2、设y=sinx,则y''=()。
- A:-sinx
- B:sinx
- C:-cosx
- D:cosx
答 案:A
解 析:y=sinx,则y'=cosx,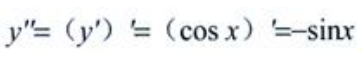 。
。
3、设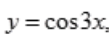 则y'=()。
则y'=()。
答 案:D
解 析: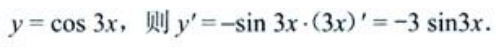
主观题
1、已知x=sint,y=cost-sint2,求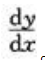 。
。
答 案:解: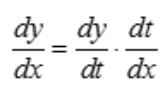 ,
,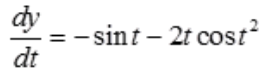 ,
,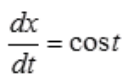 ,故
,故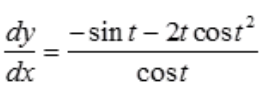 。
。
2、某厂要生产容积为V0的圆柱形罐头盒,问怎样设计才能使所用材料最省?
答 案:解:设圆柱形罐头盒的底圆半径为r,高为h,表面积为S,则 由②得
由②得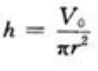 ,代入①得
,代入①得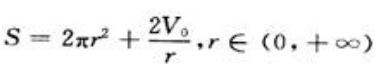
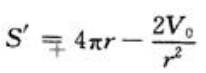 现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。
现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。
令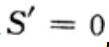 ,得
,得
由②,当 时,相应的h为:
时,相应的h为: 。
。
可见当所做罐头盒的高与底圆直径相等时,所用材料最省。
3、求由曲线y=x2(x≥0),直线y=1及y轴围成的平面图形的面积.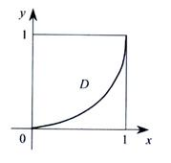
答 案:解:y=x2(x≥0),y=1及y轴围成的平面图形D如图所示.其面积为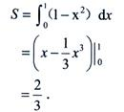
填空题
1、曲线y=1-x-x3的拐点是()。
答 案:(0,1)
解 析:y=1-x-x3,则y'=-1-3x2,y''=-6x,令y''=0得x=0,y=1。当x<0时,y''>0;x>0时,y''<0.故曲线的拐点为(0,1)。
2、微分方程y'+4y=0的通解为()。
答 案:y=Ce-4x
解 析:将微分方程分离变量,得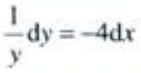 ,等式两边分别积分,得
,等式两边分别积分,得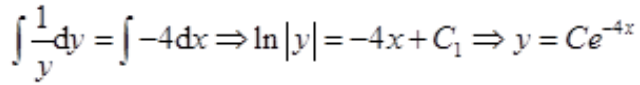
3、设f(x,y)与g(x,y)在区域D上连续,而且f(x,y)<g(x,y),则二重积分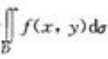 与
与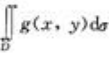 的大小关系是前者比后者()。
的大小关系是前者比后者()。
答 案:小
解 析:因为二重积分的几何意义是柱体的体积,故由f(x,y)<g(x,y)可知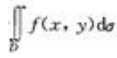 小于
小于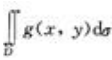 。
。
简答题
1、设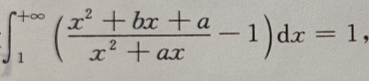 求常数a,b
求常数a,b
答 案: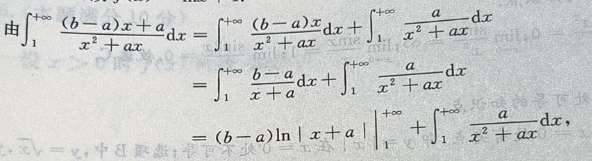 由此积分收敛知,应有b-a=0,即b=a,
由此积分收敛知,应有b-a=0,即b=a,
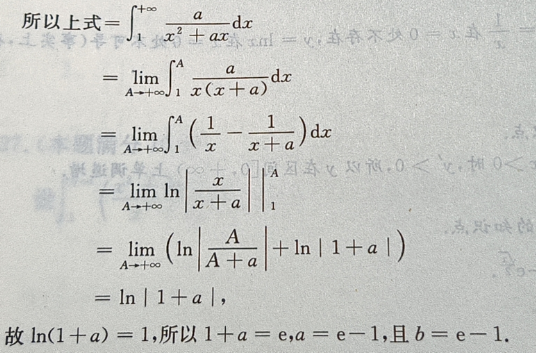
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
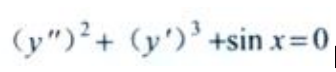 的阶数为()。
的阶数为()。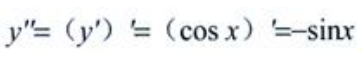 。
。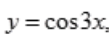 则y'=()。
则y'=()。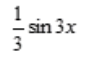
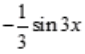
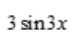
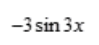
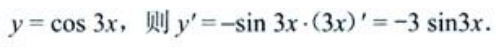
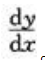 。
。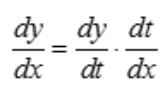 ,
,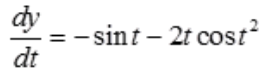 ,
,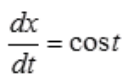 ,故
,故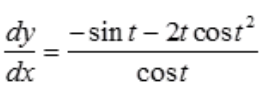 。
。 由②得
由②得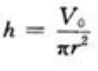 ,代入①得
,代入①得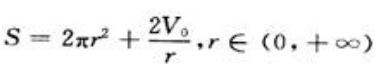
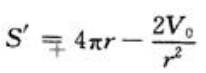 现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。
现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。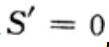 ,得
,得
 时,相应的h为:
时,相应的h为: 。
。
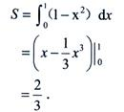
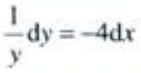 ,等式两边分别积分,得
,等式两边分别积分,得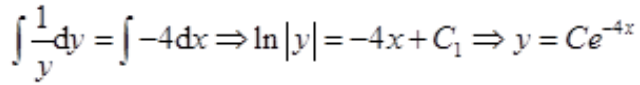
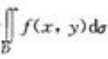 与
与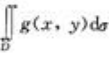 的大小关系是前者比后者()。
的大小关系是前者比后者()。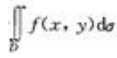 小于
小于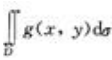 。
。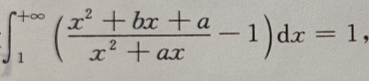 求常数a,b
求常数a,b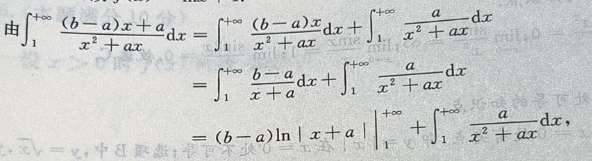 由此积分收敛知,应有b-a=0,即b=a,
由此积分收敛知,应有b-a=0,即b=a,