2024年成考专升本《高等数学二》每日一练试题06月06日

2024年成考专升本《高等数学二》每日一练试题06月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、下列命题正确的是（）.

• A：函数f(x)的导数不存在的点，一定不是f(x)的极值点
• B：若x₀为函数f(x)的驻点，则x₀必为f(x)的极值点
• C：若函数f(x)在点x₀处有极值，且f'(x₀)存在，则必有f'(x₀)＝0
• D：若函数f(x)在点x₀处连续，则f'(x₀)一定存在

答 案：C

解 析：AD两项，设f(x)＝|x|,显然x＝0是函数的极小值点，且函数在该点也连续，但函数在该点不可导；B项，设f(x)＝x³，显然x₀＝0是函数的驻点，但x₀＝0不是函数的极值点；C项，根据函数在点x₀处取极值的必要条件的定理，可知选项C是正确的.

2、设函数z=f(x²-y²),f(u)二阶可导，则=（）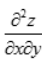  

• A：
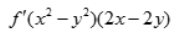
• B：
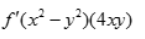
• C：
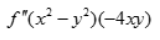
• D：

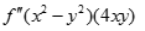
答 案：C

解 析：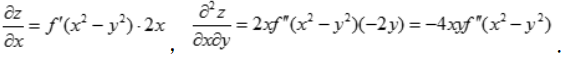

主观题

1、设函数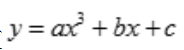，在点x＝1处取得极小值-1，且点（0,1）是该曲线的拐点，试求常数a，b，c及该曲线的凹凸区间．

答 案：解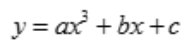：，则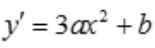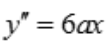，．由y(1)＝－1，y(0)＝1，y'(1)=0，得方程组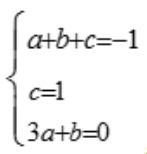，解得ａ＝１，ｂ＝－３，ｃ＝１，所以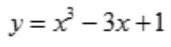，当ｘ＞０时，y''＞０，则曲线的凹区间为（０，＋∞）；当ｘ＜０时，y''＜０，则曲线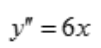的凸区间为（－∞，０）．

2、当．

答 案：证：设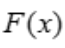＝e^x－x－1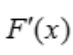，＝e^x－1．当x＜0时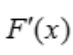，＜0，F（x）单调递减，所以当x＜0时，F（x）＞F（0）＝0，即e^x－x－1＞0，得e^x＞1＋x．

填空题

1、函数的间断点为（）．

答 案：x＝1和x＝0

解 析：分母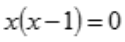时分式无意义，则x＝1和x＝0为间断点．

2、设=（）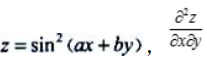  

答 案：2abcos2（ax＋by）  

解 析：

简答题

1、要做一个容积为V立方米的密闭圆柱形容器，两底面材料的价格为每平方米a元，侧面材料的价格为每平方米b元，问圆柱形容器的底面半径与高的比等于多少时，造价最低？  

答 案：设底面半径和高分别为r，h，则造价函数L=2aπr²+2bπrh,且πr²，且πr²h=V 将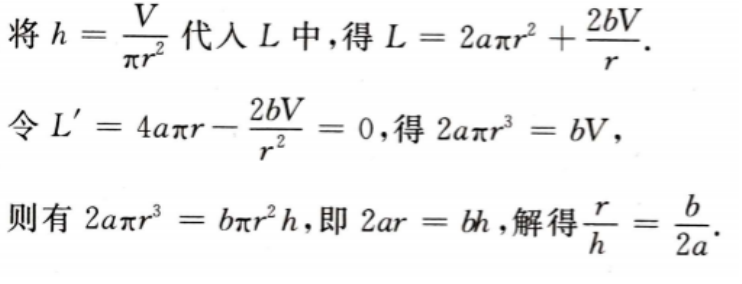 由实际问题的意义知，当底面半径与高的比为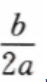时,造价最低.  

2、设D为由曲线y=x²，y=0，x=2所围成的图形. （1）求D的面积； （2）求D绕x轴旋转一周所得旋转体的体积.  

答 案：（1）D的面积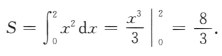 （2）D绕x轴旋转一周所得旋转体的体积