2024年成考专升本《高等数学二》每日一练试题05月17日

2024年成考专升本《高等数学二》每日一练试题05月17日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、设f(x)的一个原函数是arctanx，则f(x)的导函数是（）

• A：
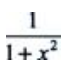
• B：
• C：
• D：

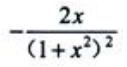
答 案：D

解 析：根据原函数的定义可知，则

2、根据f(x)的导函数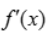的图像（如图所示），判断下列结论正确的是（ ）．

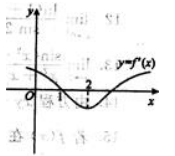
• A：在（∞，1）上f(x)是单调递减的
• B：在（∞，2）上f(x)是单调递减的
• C：f(1)为极大值
• D：f(1)为极小值

答 案：C

解 析：在x轴上方的曲线是表示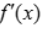>0,而x轴下方的曲线则表示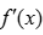<0,注在x＝1处的左边即x<1时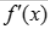>0,而2>x>1时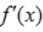<0，根据极值的第一充分条件可知f(1)为极大值．  

主观题

1、设生产某种产品的数量z与所用两种原料A的数量x吨和B的数量y吨间有关系式z＝z（x，y）＝xy，欲用100万元购买原料，已知A，B原料的单价分别为每吨1万元和每吨2万元，问购进两种原料各多少时，可使生产的产品数量最多？

答 案：解：当购进A原料x吨时，需花费x万元，此时，还可购进B原料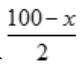吨，函数z＝xy变为关于x的一元函数，，其定义域为[0，100]．求出z'＝－x＋50，令z'＝0，即－x＋50＝0，解得x＝50．当x＜50时,z'＞0；当x＞50时,z'＜0．所以x＝50是函数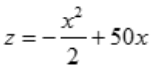的极大值点，显然也是最大值点．
此时，y＝25，即当购进A原料50吨．Ｂ原料25吨时，生产的产品数量最多．

2、计算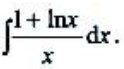

答 案：解：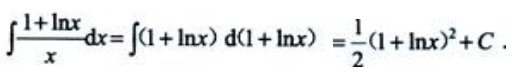

填空题

1、函数z＝2（x－y）－x²－y²的驻点坐标为（）．

答 案：（1，－1）

解 析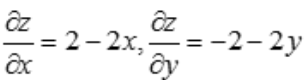：，令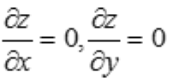，得x=1,y=-1，则函数的驻点坐标为（1，－1）．

2、函数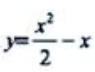的单调增加区间是（）．

答 案：（1，＋∞）

解 析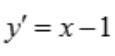：，当y'＞0，即x＞1时，函数单调增加，故函数的单调增加区间为（1，＋∞）.

简答题

1、求曲线y=x²与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.

答 案：如图所示，在x=a出切线的斜率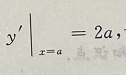为切线方程为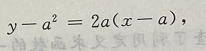

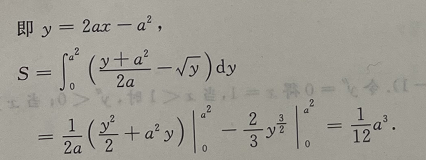
2、求函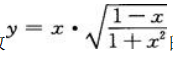数的倒数。  

答 案：等式两边同时取对数得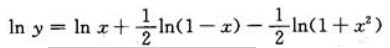 方程两边同时对x求导有 故