2024年成考专升本《高等数学一》每日一练试题05月10日

2024年成考专升本《高等数学一》每日一练试题05月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设y＝x^-2＋3,则y'|_x＝1＝（）。

• A：3
• B：-3
• C：2
• D：-2

答 案：D

解 析：y'＝（x^-2＋3）'＝（x^-2）'＋3'＝－2x^-3＝-2。

2、如果级数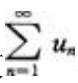收敛，那么以下级数收敛的是（）。

• A：
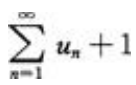
• B：
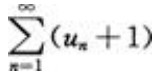
• C：
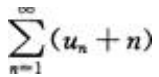
• D：

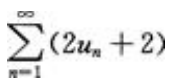
答 案：A

解 析：A项。级数收敛，则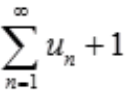收敛；由极限收敛的必要条件可知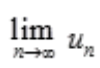，＝0，则B项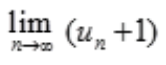，＝1；C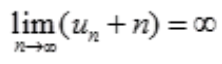项，；D项，。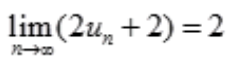

3、直线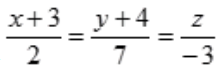与平面4x－2y－3z－3＝0的位置关系是（）。

• A：直线垂直平面
• B：直线平行平面但不在平面内
• C：直线与平面斜交
• D：直线在平面内

答 案：C

解 析：直线的方向向量s＝(2，7，－3)，且此直线过点（－3，－4，0），已知平面的法向量n＝(4,－2,－3),故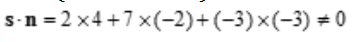，又因点（－3，－4，0）不在已知平面内，所以已知直线相交于已知平面。

主观题

1、求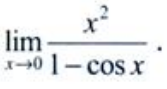

答 案：解：方法一：（洛必达法则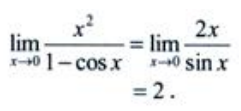）方法二：（等价无穷小）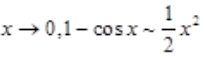

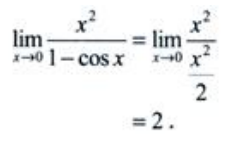
2、求微分方程的通解．

答 案：解：对应齐次微分方程的特征方程为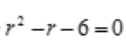，解得r₁＝3，r₂＝－2.所以齐次通解为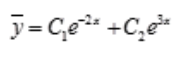。设方程的特解设为y*＝（Ax＋B）e^x，代入原微分方程可解得，A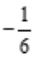＝，B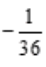＝．即非齐次微分方程特解为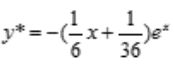。所以微分方程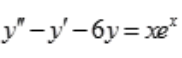的通解为。

3、欲围造一个面积为15000平方米的运动场，其正面材料造价为每平方米600元，其余三面材料造价为每平方米300元，试问正面长为多少米才能使材料费最少?

答 案：解：设运动场正面围墙长为x米，则宽为，设四面围墙高相同，记为h，则四面围墙所用材料费用，f（x）为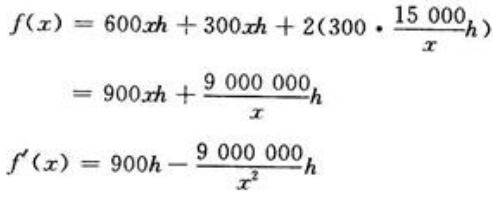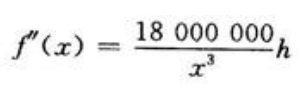令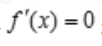得驻点x₁＝100，x₂＝－100（舍掉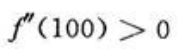），由于驻点唯一，且实际问题中存在最小值，可知x＝100米，侧面长150米时，所用材料费最小。

填空题

1、交换二次积分的积分次序，（）。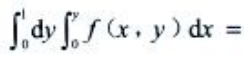

答 案：

解 析：由题设有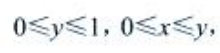从而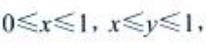故交换次序后二次积分为。

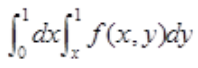2、极限＝（）。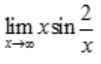

答 案：2

解 析：。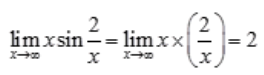

3、＝（）。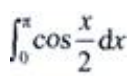

答 案：2

解 析：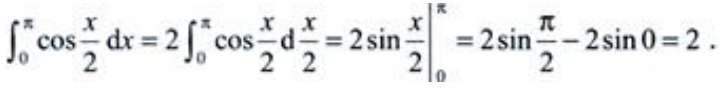

简答题

1、求微分方程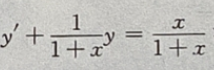满足初值条件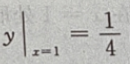的特解  

答 案：