2024年成考专升本《高等数学一》每日一练试题03月29日
2024-03-29 11:22:29 来源:吉格考试网
2024年成考专升本《高等数学一》每日一练试题03月29日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设f(x,y)为连续函数,则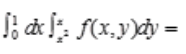 ()。
()。
- A:
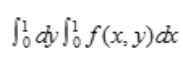
- B:
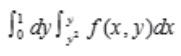
- C:
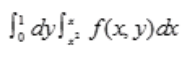
- D:
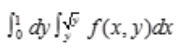
答 案:D
解 析:积分区域D可以由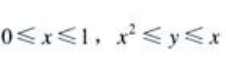 表示,其图形为图中阴影部分
表示,其图形为图中阴影部分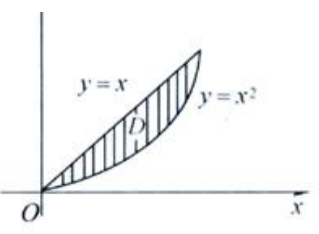 。也可以将D表示为
。也可以将D表示为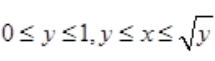 ,故二重积分也可表示为
,故二重积分也可表示为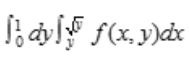 。
。
2、下列等式成立的是()
- A:
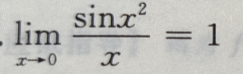
- B:
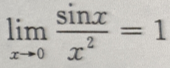
- C:
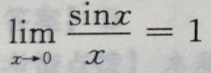
- D:
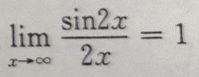
答 案:C
解 析:由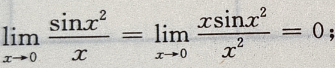
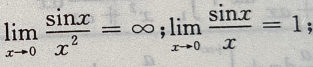
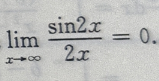
3、在空间直角坐标系中方程y2=x表示的是()。
- A:抛物线
- B:柱面
- C:椭球面
- D:平面
答 案:B
解 析:空间中,缺少一维坐标的方程均表示柱面,y2=x是母线平行于z轴的柱面。
主观题
1、求微分方程 的通解.
的通解.
答 案:解:对应齐次微分方程的特征方程为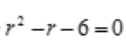 ,解得r1=3,r2=-2.所以齐次通解为
,解得r1=3,r2=-2.所以齐次通解为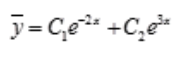 。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=
。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=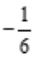 ,B=
,B=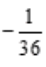 .即非齐次微分方程特解为
.即非齐次微分方程特解为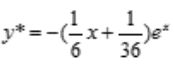 。所以微分方程
。所以微分方程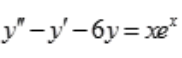 的通解为
的通解为 。
。
2、求y'+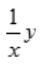 =1的通解.
=1的通解.
答 案:解:
3、求函数y=xex的极小值点与极小值
答 案:解:方法一: 令y'=0,得x=-1。
令y'=0,得x=-1。
当x<-1时,y'<0;当x>-1时,y'>0。
故极小值点为x=-1,极小值为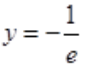 。
。
方法二:,
令y'=0,得x=-1,又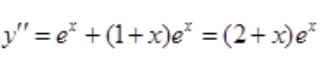 ,
, 。
。
故极小值点为x=-1,极小值为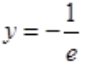 。
。
填空题
1、幂级数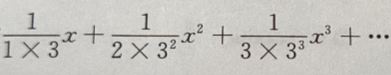 的收敛半径为()
的收敛半径为()
答 案:3
解 析:所给幂级数通项为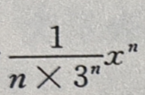 则
则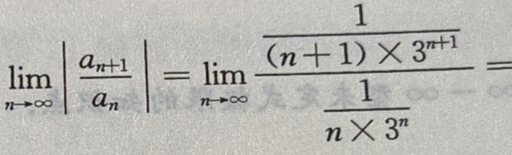
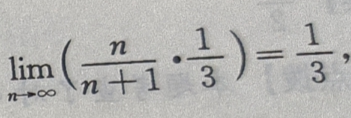 所以收敛半径R=3
所以收敛半径R=3
2、过原点且垂直于y轴的平面方程为()。
答 案:y=0
解 析:过原点且垂直于y轴的平面即x轴所在的平面,方程为y=0。
3、设y=f(x)可导,点x0=2为f(x)的极小值点,且f(2)=3,则曲线y=f(x)在点(2,3)处的切线方程为()。
答 案:y=3
解 析:由于y=f(x)可导,且点x0=2为f(x)的极小值点,由极值的必要条件可得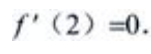 又f(2)=3,可知曲线过点(2,3)的切线方程为
又f(2)=3,可知曲线过点(2,3)的切线方程为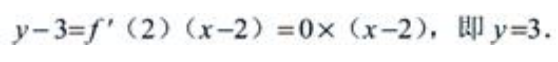
简答题
1、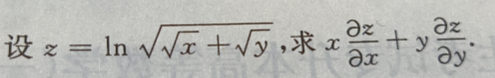
答 案: