2024年成考专升本《高等数学一》每日一练试题01月16日
2024-01-16 11:28:16 来源：吉格考试网
2024年成考专升本《高等数学一》每日一练试题01月16日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、设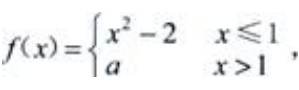
在x＝1连续，则a＝（）。
- A：-2
- B：-1
- C：1－e
- D：2
答 案：B
解 析：函数f（x）为分段函数，且在x＝1处连续，故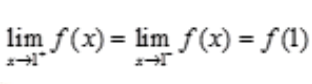
，
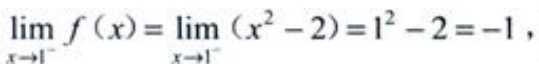
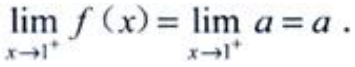因此a＝-1。
2、下列四个点钟，在平面x+y-z+2=0上的是（）
- A：(-2,1,1)
- B：(0,1,1)
- C：(1,0,1)
- D：(1,1,0)
答 案：A
解 析：把选项中的几个点带入平面方程,只有选项 A 满足方程,故选项 A是平面上的点.
3、过点（1，0，0），（0，1，0），（0，0，1）的平面方程为（）。
- A：x＋y＋z＝1
- B：2x＋y＋z＝1
- C：x＋2y＋z＝1
- D：z＋y＋2z＝1
答 案：A
解 析：方法一：设所求平面方程为Ax＋By＋Cz＋D＝0.由于点（1，0，0），（0，1，0），（0，0，1）在平面上，将上述三点坐标分别代入所设方程，可得A＋D＝0，B＋D＝0，C＋D＝0，即A＝B＝C＝-D，再代回方程可得x＋y＋z＝1。方法二：由于点（1，0，0），（0，1，0），（0，0，1）分别位于x轴、y轴、z轴上，可由平面的截距式方程得出x＋y＋z＝1即为所求平面方程。
主观题
1、计算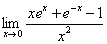
答 案：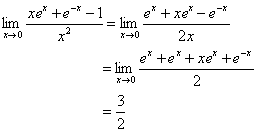
2、设ex＋x＝ey＋y，求
。
答 案：解：对等式两边同时微分，得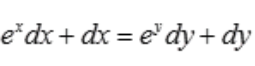
，故
。
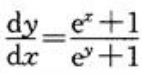3、求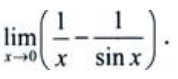
答 案：解：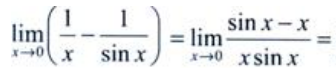
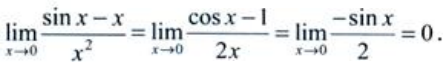
填空题
1、若级数
条件收敛（其中k＞0为常数），则k的取值范围是（）。
答 案：0＜k≤l
解 析：k＞1时，级数各项取绝对值，得正项级数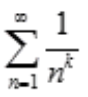
，是收敛的p级数，从而原级数绝对收敛；当0＜k≤l时，由莱布尼茨交错级数收敛性条件可判明原级数条件收敛，因此应有0＜k≤1。
2、设函数x=3x+y2,则dz=（）。
答 案：3dx+2ydy
解 析：
3、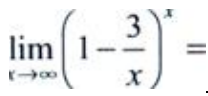
（）。
答 案：e-3
解 析：所给极限为重要极限的形式，由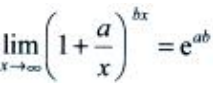
，可得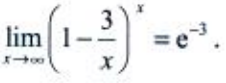
简答题
1、函数y=y(x)由方程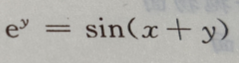
确定，求dy
答 案：
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
