2024年成考专升本《高等数学一》每日一练试题01月07日

2024年成考专升本《高等数学一》每日一练试题01月07日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若级数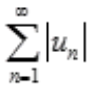收敛，则（）。

• A：发散
• B：条件收敛
• C：绝对收敛
• D：无法判定敛散性

答 案：C

解 析：级数绝对收敛的性质可知，收敛，则收敛，且为绝对收敛。

2、下列各点在球面（x－1）²＋y²＋（z－1）²＝1上的是（）。

• A：（1，0，1）
• B：（2，0，2）
• C：（1，1，1）
• D：（1，1，2）

答 案：C

解 析：将各个点代入球面公式可知（1，1，1）在球面上。

3、（）。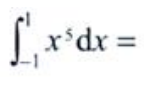

• A：
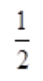
• B：
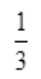
• C：
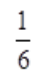
• D：0

答 案：D

解 析：被积函数x⁵为奇函数，积分区间[1，1]为对称区间，由定积分对称性质可知。

主观题

1、求。

答 案：解：。

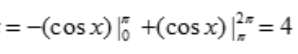2、证明：当x＞0时，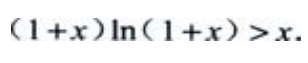

答 案：证：设f（x）＝（1＋x）ln（1＋x）－x，则f'（x）＝ln（1＋x）。当x＞0时，f'（x）＝ln（1＋x）＞0，故f（x）在（0，＋∞）内单调增加，
且f（0）＝0，故x＞0时，f（x）＞0，
即（1＋x）Ln（1＋x）－x＞0，（1＋x）ln（1＋x）＞x。

3、求微分方程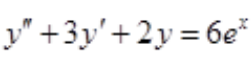的通解．

答 案：解：原方程对应的齐次方程为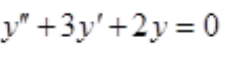。特征方程为，r²＋3r＋2＝0，特征值为r₁＝-2，r₂＝-1。齐次方程的通解为y＝C₁e^-2x＋C₂e^-x。
设特解为y*＝Aex，代入原方程有6A＝6，得A＝1。
所以原方程的通解为y＝C₁e^-2x＋C₂e^-X＋e^x（C1，C2为任意常数）。

填空题

1、曲线y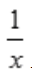＝与直线y＝x，x＝2围成的图形面积为（）。

答 案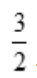：－1n2

解 析：由题作图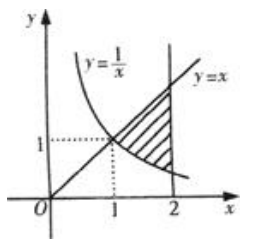，由图可知所求面积为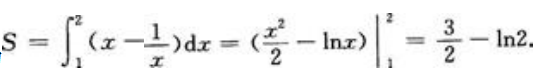

2、设y＝(x＋3)²，则y'＝（）。

答 案：2(x＋3)

解 析：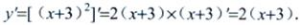

3、设函数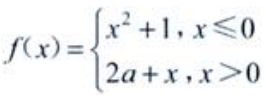，在x＝0处连续，则a＝（）。

答 案：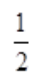

解 析：由于f（x）在点x＝0处连续，故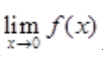存在，且，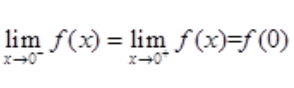

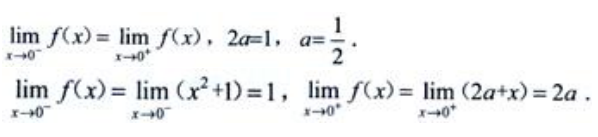
简答题

1、给定曲线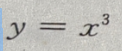与直线y=px-q（其中p>0），求p与q为关系时，直线y=px-q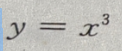的切线。

答 案：由题意知，再切点处有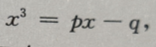两边对x求导得