2023年成考专升本《高等数学二》每日一练试题12月17日
2023-12-17 11:26:58 来源:吉格考试网
2023年成考专升本《高等数学二》每日一练试题12月17日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、已知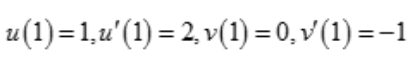 ,若函数
,若函数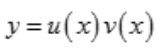 ,则y'(1)等于().
,则y'(1)等于().
- A:-2
- B:-1
- C:1
- D:2
答 案:B
解 析:根据函数积的求导法则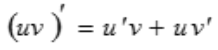 ,有
,有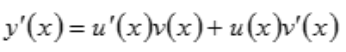 ,所以
,所以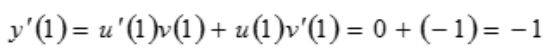
2、 ().
().
- A:x2+ex+C
- B:2x2+ex+C
- C:x2+xex+C
- D:2x2+xex+C
答 案:A
解 析:根据不定积分加法原则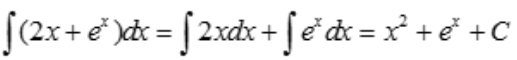 .
.
主观题
1、一批零件中有10个合格品和2个废品,安装机器时,从这批零件中任取一个,如果每次取出废品后不再放回,用X表示在取得合格品以前已取出的废品数,求:(1)随机变量X的分布列;
(2)随机变量X的分布函数.
答 案:解:(1)由题意知,随机变量X的可能值是0,1,2,且有 随机变量x的分布列为
随机变量x的分布列为 (2)随机变量X的分布函数为
(2)随机变量X的分布函数为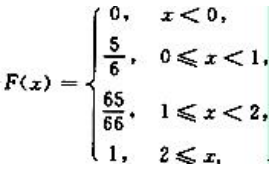
2、设平面图形是由曲线y= 和x+y=4围成的.(1)求此平面图形的面积S.
和x+y=4围成的.(1)求此平面图形的面积S.
(2)求此平面图形绕x轴旋转而成的旋转体的体积Vx.
答 案:解:曲线y= 和x+y=4围成的图形如图阴影部分所示
和x+y=4围成的图形如图阴影部分所示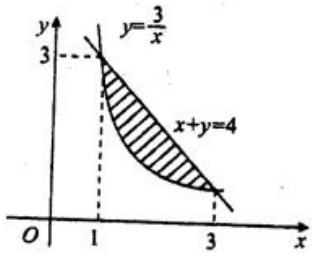 .求两条曲线的交点,解方程
.求两条曲线的交点,解方程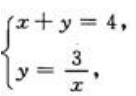 得交点(1,3)与(3,1).(1)面积
得交点(1,3)与(3,1).(1)面积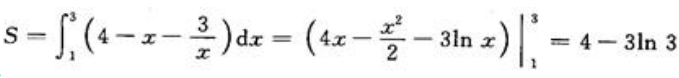 ;
;
(2)旋转体体积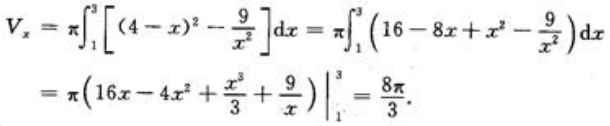
填空题
1、曲线y=2x2在点(1,2)处的切线方程为y=().
答 案:4x-2
解 析: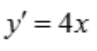 ,
,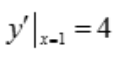 ,故切线方程为
,故切线方程为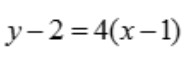 ,即
,即 .
.
2、曲线y=lnx在点(1,0)处的切线方程为()
答 案:y=x-1
解 析:因为y=lnx,y'=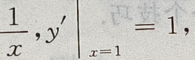 所以曲线y=lnx在点(1,0)处的切线方程为y=x-1
所以曲线y=lnx在点(1,0)处的切线方程为y=x-1
简答题
1、求由曲线y=x2与x=2,y=0所围成图形分别绕x轴,y轴旋转一周所生成的旋转体体积.
答 案: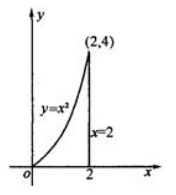
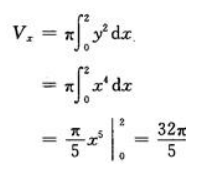 绕y轴旋转一周所得的旋转体体积为
绕y轴旋转一周所得的旋转体体积为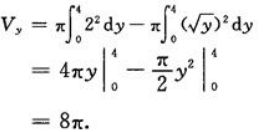
2、已知曲线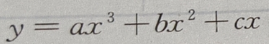 在点(1,2)处有水平切线,且原点为该曲线的拐点,求a,b,c的值,并写出此曲线的方程。
在点(1,2)处有水平切线,且原点为该曲线的拐点,求a,b,c的值,并写出此曲线的方程。
答 案:
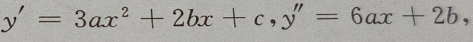 由已知条件得:
由已知条件得:
 故b=0,a=-1,c=3,次曲线的方程为
故b=0,a=-1,c=3,次曲线的方程为



