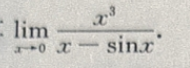课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2023年成考专升本《高等数学一》每日一练试题11月22日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、当x→0时,与3x2+2x3等价的无穷小量是()。
答 案:B
解 析:由于当x→0时,3x2为x的二阶无穷小量,2x3为x的三阶无穷小量,因此3x2+2x3为x的二阶无穷小量,即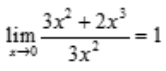 。
。
2、设f(x)为连续函数,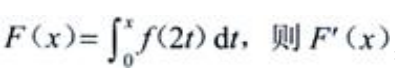 =()。
=()。
- A:f(2x)
- B:2f(x)
- C:-f(2x)
- D:-2f(x)
答 案:A
解 析:f(x)为连续函数,由可变上限积分求导公式可得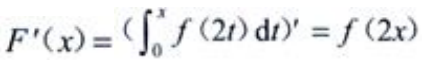 。
。
3、设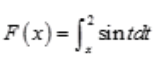 ,则F′(x)=()。
,则F′(x)=()。
- A:sinx+sin2
- B:-sinx+sin2
- C:sinx
- D:-sinx
答 案:D
解 析:由可变限积分求导公式可知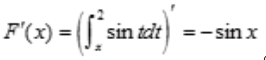 。
。
主观题
1、求微分方程 的通解.
的通解.
答 案:解:对应齐次微分方程的特征方程为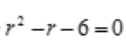 ,解得r1=3,r2=-2.所以齐次通解为
,解得r1=3,r2=-2.所以齐次通解为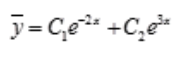 。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=
。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=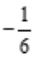 ,B=
,B=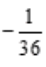 .即非齐次微分方程特解为
.即非齐次微分方程特解为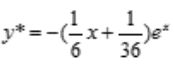 。所以微分方程
。所以微分方程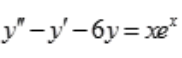 的通解为
的通解为 。
。
2、求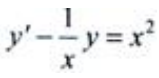 .
.
答 案:解:微分方程的通解为
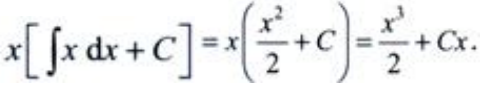
3、设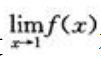 存在且
存在且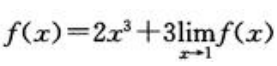 ,求
,求
答 案:解:设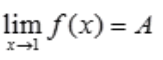 对
对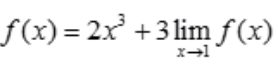 两边同时求极限,得
两边同时求极限,得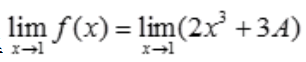 ,即
,即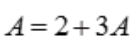 ,得
,得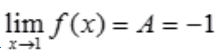 。
。
填空题
1、过点M0(0,0,0)且与直线 平行的直线方程为()。
平行的直线方程为()。
答 案:
解 析:所给直线的方向向量为(1,2,-1).所求直线与已给直线平行,则可取所求直线方向向量为(1,2,-1).由于所求直线过原点(0,0,0),由直线的点向式方程可知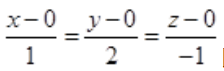 即为所求直线方程。
即为所求直线方程。
2、设f(x,y)与g(x,y)在区域D上连续,而且f(x,y)<g(x,y),则二重积分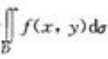 与
与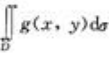 的大小关系是前者比后者()。
的大小关系是前者比后者()。
答 案:小
解 析:因为二重积分的几何意义是柱体的体积,故由f(x,y)<g(x,y)可知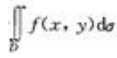 小于
小于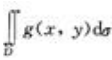 。
。
3、设F(x,y,z)=0,其中z为x,y的二元函数,F(x,y,z)对x,y,z存在连续偏导数,且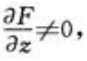 则
则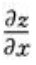 =()。
=()。
答 案: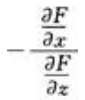
解 析:根据复合函数求偏导法则可得: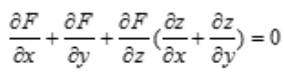 ,要求z对x的偏导,则把y看做常数,所以有
,要求z对x的偏导,则把y看做常数,所以有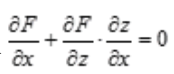 ,所以
,所以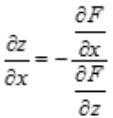 。
。
简答题
1、计算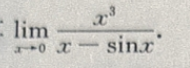
答 案: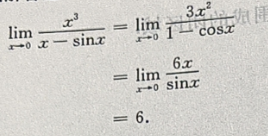
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
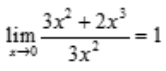 。
。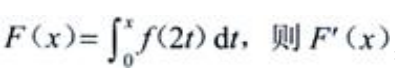 =()。
=()。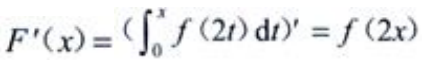 。
。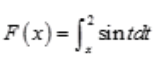 ,则F′(x)=()。
,则F′(x)=()。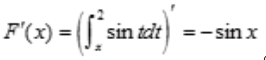 。
。 的通解.
的通解.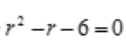 ,解得r1=3,r2=-2.所以齐次通解为
,解得r1=3,r2=-2.所以齐次通解为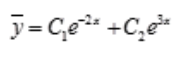 。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=
。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=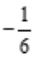 ,B=
,B=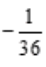 .即非齐次微分方程特解为
.即非齐次微分方程特解为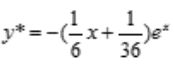 。所以微分方程
。所以微分方程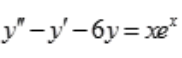 的通解为
的通解为 。
。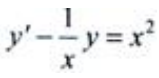 .
.
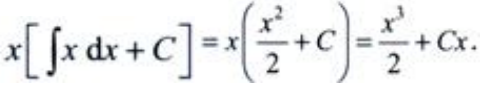
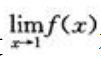 存在且
存在且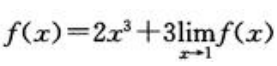 ,求
,求
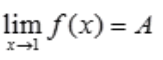 对
对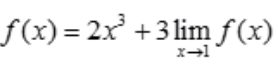 两边同时求极限,得
两边同时求极限,得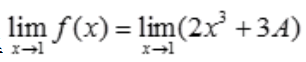 ,即
,即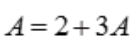 ,得
,得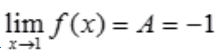 。
。 平行的直线方程为()。
平行的直线方程为()。
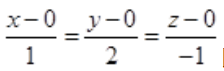 即为所求直线方程。
即为所求直线方程。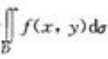 与
与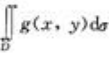 的大小关系是前者比后者()。
的大小关系是前者比后者()。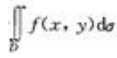 小于
小于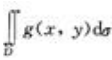 。
。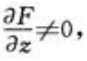 则
则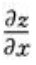 =()。
=()。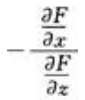
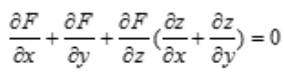 ,要求z对x的偏导,则把y看做常数,所以有
,要求z对x的偏导,则把y看做常数,所以有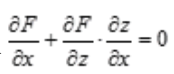 ,所以
,所以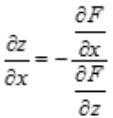 。
。