2023年成考专升本《高等数学一》每日一练试题11月11日
2023-11-11 11:25:54 来源:吉格考试网
2023年成考专升本《高等数学一》每日一练试题11月11日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列等式成立的是()。
- A:
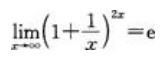
- B:
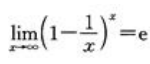
- C:
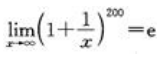
- D:
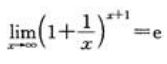
答 案:D
解 析:A项,由 ,可知
,可知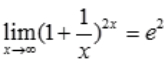 ;B项,
;B项, ;C项,
;C项,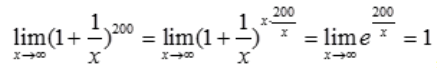 ;D项,
;D项, 。
。
2、函数 的单调减区间为()。
的单调减区间为()。
- A:(-∞,-2)
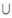 (-2,+∞)
(-2,+∞) - B:(-2,2)
- C:(-∞,0)
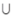 (0,+∞)
(0,+∞) - D:(-2,0)
 (0,2)
(0,2)
答 案:D
解 析:由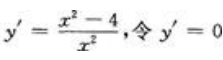 ,得驻点为x=±2,而不可导点为x=0,列表讨论如下:
,得驻点为x=±2,而不可导点为x=0,列表讨论如下: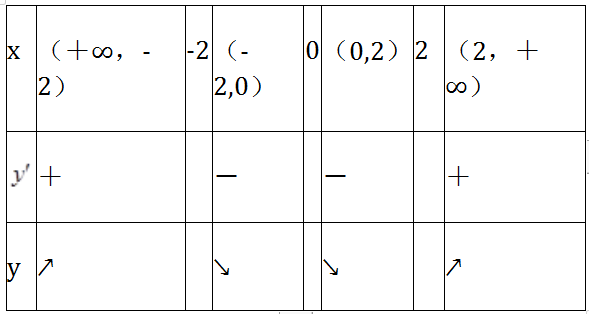 故单调减区间为(-2,0)
故单调减区间为(-2,0) (0,2)。
(0,2)。
3、设y=f(x)在点x0的某邻域内可导,且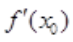 =0,则点x0一定是()。
=0,则点x0一定是()。
- A:极大值点
- B:极小值点
- C:驻点
- D:拐点
答 案:C
解 析:极值点是函数某段子区间的最值,一般在驻点或者不可导点取得;驻点是函数一阶导数为0的点对应的x值;拐点是凸曲线与凹曲线的连接点,当函数图像上的某点使函数的二阶导数为零,且三阶导数不为零时,这点即为函数的拐点;综上所述,点x0为该函数的驻点。
主观题
1、将 展开为x的幂级数.
展开为x的幂级数.
答 案:解:因为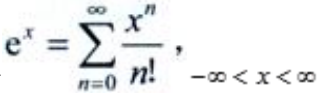 ,所以
,所以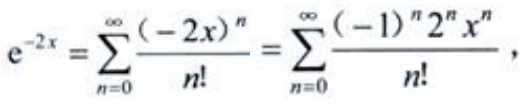
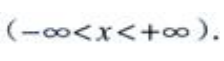
2、证明:当x>0时,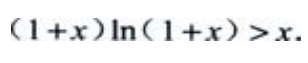
答 案:证:设f(x)=(1+x)ln(1+x)-x,则f'(x)=ln(1+x)。当x>0时,f'(x)=ln(1+x)>0,故f(x)在(0,+∞)内单调增加,
且f(0)=0,故x>0时,f(x)>0,
即(1+x)Ln(1+x)-x>0,(1+x)ln(1+x)>x。
3、求过点M0(0,2,4),且与两个平面π1,π2都平行的直线方程,其中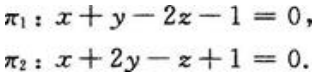
答 案:解:如果直线l平行于π1,则平面π1的法线向量n1必定垂直于直线l的方向向量s.同理,直线l平行于π2,则平面π2的法线向量n2必定满足n2⊥s.由向量积的定义可知,取 由于直线l过点M0(0,2,4),由直线的标准方程可知
由于直线l过点M0(0,2,4),由直线的标准方程可知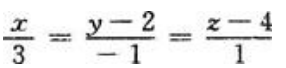 为所求直线方程。
为所求直线方程。
填空题
1、设F(x,y,z)=0,其中z为x,y的二元函数,F(x,y,z)对x,y,z存在连续偏导数,且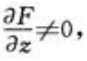 则
则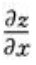 =()。
=()。
答 案: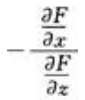
解 析:根据复合函数求偏导法则可得: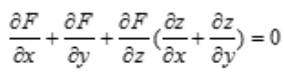 ,要求z对x的偏导,则把y看做常数,所以有
,要求z对x的偏导,则把y看做常数,所以有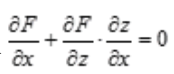 ,所以
,所以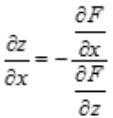 。
。
2、曲线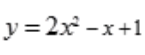 在点(1,2)处的切线方程为()。
在点(1,2)处的切线方程为()。
答 案:y-2=3(x-1)
解 析:y=2x2-x+1点(1,2)在曲线上,且 ,因此曲线过点(1,2)的切线方程为y-2=3(x-1),或写为y=3x-1。
,因此曲线过点(1,2)的切线方程为y-2=3(x-1),或写为y=3x-1。
3、微分方程y'+4y=0的通解为()。
答 案:y=Ce-4x
解 析:将微分方程分离变量,得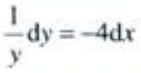 ,等式两边分别积分,得
,等式两边分别积分,得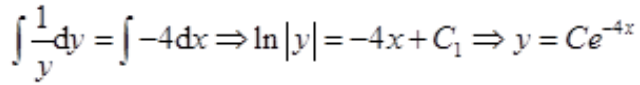
简答题
1、求曲线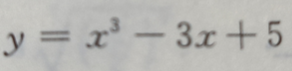 的拐点;
的拐点;
答 案:



