2023年成考专升本《高等数学二》每日一练试题10月16日

2023年成考专升本《高等数学二》每日一练试题10月16日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、设函数z＝e^x＋y²，则（）.

• A：2y
• B：e^x＋2y
• C：e^x＋y²
• D：e^x

答 案：D

解 析：当对x求导时，y相当于常量，故，.

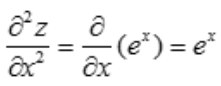2、掷两粒骰子，出现点数之和为5的概率为（）.

• A：
• B：
• C：
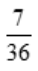
• D：

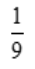
答 案：D

解 析：总的样本点为6×6＝36个，点数之和为5的有（1，4），（2，3），（3，2），（4，1）共4个样本点，所求概率为.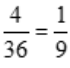

主观题

1、求函数f(x)＝的单调区间、极值和曲线y＝f(x)的凹凸区间．

答 案：解：函数的定义域为（－∞，＋∞）．求导得y'＝x²－4，y''＝2x令y'＝0，得x＝±2．y''＝0，得x＝0．
函数f(x)的单调增区间为（－∞，－2），（2，＋∞），函数f(x)的单调减区间为（－2，2）；
函数的极大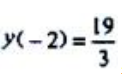值为，极小值为；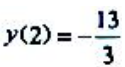
曲线的凸区间为（－∞，0），曲线的凹区间为（0，＋∞）．

2、袋中有4张卡片，上面分别写有从1～4四个整数．让甲乙两人各自从中挑选一张，甲先挑选：选完后卡片不放回，同时再放入一张写有数字5的卡片，接下来让乙去挑选．记乙挑得的数字为X．试求随机变量X的概率分布，并求数学期望E(X)．

答 案：解：（1）随机变量X的可能取值为1，2，3，4，5．显然P(X＝1)＝P(X＝2)＝P(X＝3)＝P(X＝4)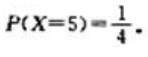，设事件A为甲挑到写有数字1的卡片，则．
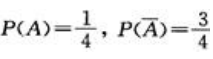事件B为乙挑到写有数字1的卡片，则P(B)＝P(X＝1)，因此
易知P(B|A)＝0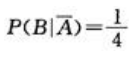，，因此．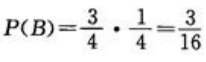
所以离散型随机变量X的概率分布为：
（2）．

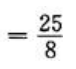填空题

1、函数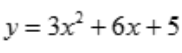的单调减少区间是（）．

答 案：（－∞，－1）

解 析：函数的定义域为（－∞，＋∞）．令，解得驻点ｘ＝－1．在区间（－∞，－1）内，y'＜0，函数单调减少；在区间（－1，＋∞）内，y'＞0，函数单调增加．

2、袋中装有数字为1、2、3、4的4个球，从中任取2个球，设事件A＝{2个球上的数字和≥5}，则P（A）＝（）．

答 案：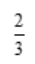

解 析：4个球中任取2个球共有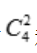种情况；2个球上的数字和≥5包括：最大数为4时有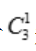种情况；最大数为3时有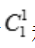种情况．所以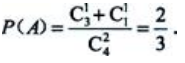

简答题

1、设函数求常数a。使f(x)在点x=0处连续。  

答 案： 要f(x)在点x=0处连续，则需所以a=1.

2、设函数y=sin²x,求  

答 案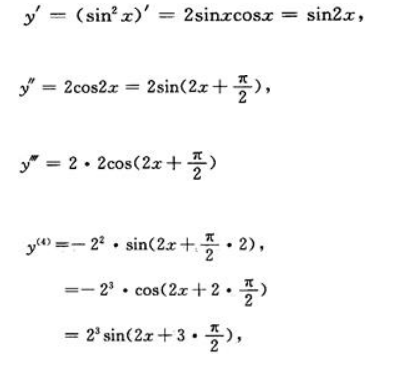： 所以