2023年成考专升本《高等数学二》每日一练试题10月07日

2023年成考专升本《高等数学二》每日一练试题10月07日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、根据f(x)导函数f'(x)的图像，判定下列结论正确的是（）.

• A：在（-∞，1）内，f(x)是单调增加的
• B：在（-∞，0）内，f(x)是单调增加的
• C：f(-1)为极大值
• D：f(-1)为极小值

答 案：D

解 析：x轴上方的f'(x)＞0，x轴下方的f'(x)＜0.即当x＜-1时，f'(x)＜0；当x＞-1时，根据极值的第一充分条件，可知f(-1)为极小值.

2、曲线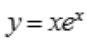的拐点坐标是（）.

• A：（0，1）
• B：（1，e）
• C：
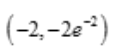
• D：

答 案：C

解 析：，，令y''=0，得x=-2，.当x＜－2时，y''＜0，y为凸函数；当x＞－2时，y''＞0，y为凹函数，所以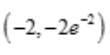为曲线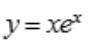的拐点坐标.

主观题

1、计算．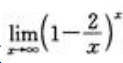

答 案：解：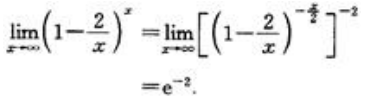

2、求函数f(x,y)＝x²＋y²在条件2x＋3y＝1下的极值．

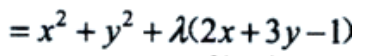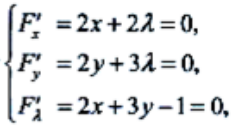答 案：解：求条件极值，作拉普拉斯辅助函数F（x，y，λ）＝f(x,y)＋λ（2x＋3y－1）令得．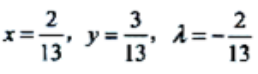
因此，f(x,y)在条件2x＋3y＝1下的极值为．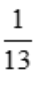

填空题

1、设函数f(x)在x＝2处连续，且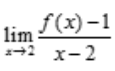存在，则f(2)＝（）．

答 案：1

解 析：因为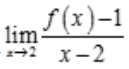存在，所以，即．因为f(x)在x＝2处连续，所以f(2)＝1.

2、（）．

答 案：

解 析：因为积分区间关于原点对称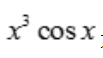，是奇函数，故，则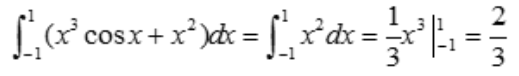

简答题

1、证明：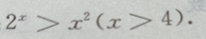

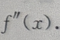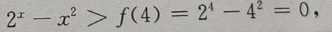答 案：令则由于此式不便判定符号，故再求出又因所以f'(x)单调增加，故f'(x)>f'(4)=-8=8(2ln2-1)=8(ln4-1)>0, 得到f(x)单调增加，故f(x)>f(4),即因此

2、从一批有10件正品及2件次品的产品中，不放回地一件一件地抽取产品，设每个产品被抽到的可能性相同，求直到取出正品为止所需抽取的次数X的概率分布。  

答 案：由题意，X的所有可能的取值为1,2,3， X=1，即第一次就取到正品，P{X=1}=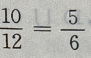 X=2，即第一次取到次品且第二次取到正品，P{X=2}= 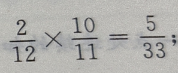同理，P{X=3}= 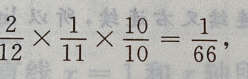故X的概率分布如下