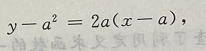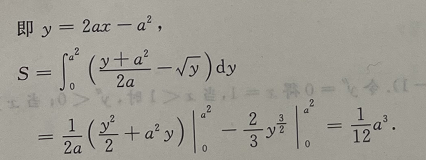课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2023年成考专升本《高等数学二》每日一练试题09月25日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设离散型随机变量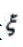 的分布列为
的分布列为 ,则
,则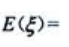 ().
().
答 案:A
解 析: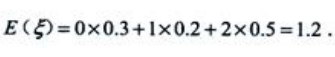
2、函数f(x)在[0,2]上连续,且在(0,2)内f'(x)>0,则下列不等式成立的是().
- A:f(0)>f(1)>f(2)
- B:f(0)<f(1)<f(2)
- C:f(0)<f(2)<f(1)
- D:f(0)>f(2)>f(1)
答 案:B
解 析:由题意知函数f(x)在(0,2)内单调递增,故f(0)<f(1)<f(2).
主观题
1、计算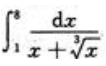 .
.
答 案:解:设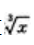 =t,得x=t3,所以dx=3t2dt当x=1时,t=1;当x=8时,t=2.所以
=t,得x=t3,所以dx=3t2dt当x=1时,t=1;当x=8时,t=2.所以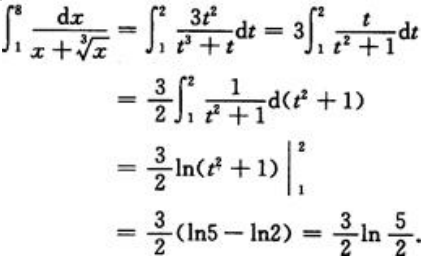
2、甲袋中有15只乒乓球,其中3只白球,7只红球,5只黄球,乙袋中有20只乒乓球,其中10只白球,6只红球,4只黄球.现从两袋中各取一只球,求两球颜色相同的概率.
答 案:解:样本空间的样本点应该是甲、乙两袋中的样本点之积,也就是从甲袋中取一个球再从乙袋中取一球的所有取法,即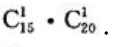 两球颜色相同的情况有三种,因此其样本点共有
两球颜色相同的情况有三种,因此其样本点共有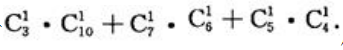 所以两球颜色相同的概率为
所以两球颜色相同的概率为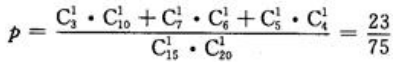
填空题
1、 ().
().
答 案:e3
解 析:利用重要极限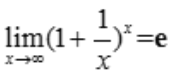 ,得
,得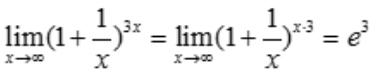 .
.
2、设y'=2x,且x=1时,y=2,则y=().
答 案:x2+1
解 析:由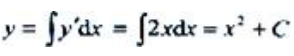 ,又由初值条件,有y(1)=1+C=2,得C=1.故y=x2+1.
,又由初值条件,有y(1)=1+C=2,得C=1.故y=x2+1.
简答题
1、已知函数f(x)=ax3-bx2+cx在区间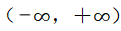 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值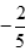 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
答 案:f(x)=ax3-bx2+cx,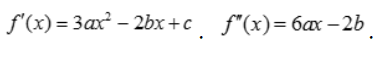 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
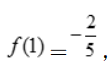 即a+c=
即a+c=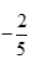 ,
,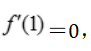 得3a+c=0.解得a=
得3a+c=0.解得a=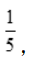 c=
c= 此时
此时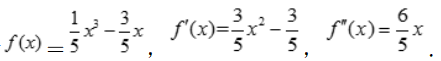 令
令 得
得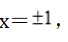
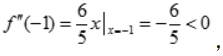 所以
所以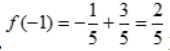 为极大值,
为极大值,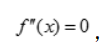 得x=0,x<0时,
得x=0,x<0时,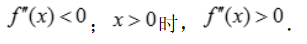 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.
2、求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.
答 案:如图所示,在x=a出切线的斜率为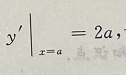 切线方程为
切线方程为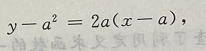

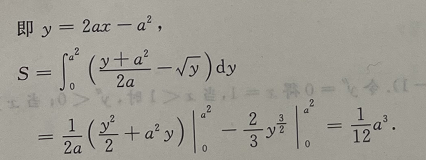
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
 ,则
,则 。()
。()
 所以
所以
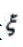 的分布列为
的分布列为 ,则
,则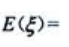 ().
().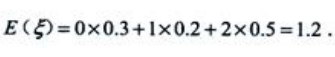
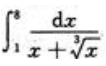 .
.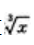 =t,得x=t3,所以dx=3t2dt当x=1时,t=1;当x=8时,t=2.所以
=t,得x=t3,所以dx=3t2dt当x=1时,t=1;当x=8时,t=2.所以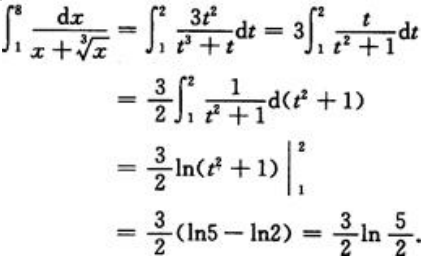
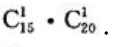 两球颜色相同的情况有三种,因此其样本点共有
两球颜色相同的情况有三种,因此其样本点共有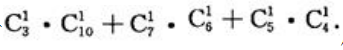 所以两球颜色相同的概率为
所以两球颜色相同的概率为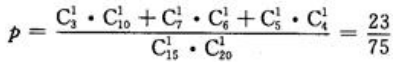
 ().
().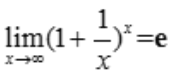 ,得
,得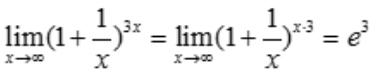 .
.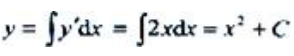 ,又由初值条件,有y(1)=1+C=2,得C=1.故y=x2+1.
,又由初值条件,有y(1)=1+C=2,得C=1.故y=x2+1.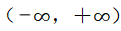 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值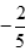 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
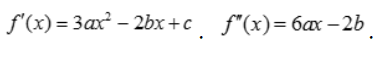 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
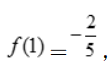 即a+c=
即a+c=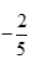 ,
,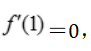 得3a+c=0.解得a=
得3a+c=0.解得a=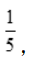 c=
c= 此时
此时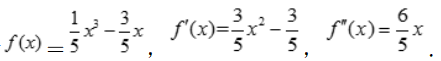 令
令 得
得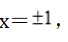
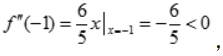 所以
所以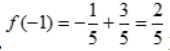 为极大值,
为极大值,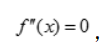 得x=0,x<0时,
得x=0,x<0时,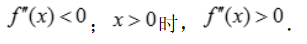 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.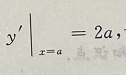 切线方程为
切线方程为