2022年成考高起点《数学(文史)》每日一练试题08月23日

2022年成考高起点《数学(文史)》每日一练试题08月23日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

2、

• A：
• B：
• C：
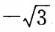
• D：

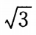
答 案：A

3、函数y=cos4x的最小正周期为（）

• A：
• B：
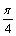
• C：π
• D：2π

答 案：A

解 析：函数y=-cos4x的最小正周期.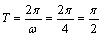

4、下列函数中，在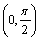为减函数的是（）

• A：y=ln(3x+1)
• B：y=x+1
• C：y=5sinx
• D：y=4-2x

答 案：D

解 析：A、B选项在其定义域上为增函数，选项C在上为增函数，只有D选项在实数域上为减函数.

主观题

1、(I)求{a_n}的通项公式; 　　

答 案：a_2??=1/2+d??,??a_5??=1/2+4d 由已知得(1/2+d)²=1/2(1/2+4d) 解得d=0(舍去)，d或=1. 所以{a_n｝的通项公式为 a_n=1/2+(n-1)×1=n-1/2 ???_?

2、已知抛物线经过点(2，3)，对称轴方程为x=1，且在x轴上截得的弦长为4，试求抛物线的解析式。

答 案：设抛物线y=a(x-x1)(x-x2)，与x轴的两交点为A(x1，0)，B(x2，0)，由｜AB｜=4，对称轴为x=1得x1=1-2=-1，x2=1+2=3，∴y=a(x+1)(x-3)，又∵抛物线过点(2，3)，∴3=a(2+1)(2-3)，得a=-1，故所求的抛物线方程为y=-(x+1)(x-3)，即y=-x²+2x+3。

3、(Ⅱ)△ABC的面积. 　　 

答 案：设CD为AB边上的高，那么 CD=ACsin30°=1/2, △ABC的面积为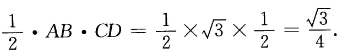

4、已知等差数列{a_n}中，a₃+a₄+a₅=6。
（Ⅰ）求a₄的值；
（Ⅱ）若a₁=-4，求{a_n}的通项公式。

答 案：（Ⅰ）由等差数列的基本性质，a₃+a₄+a₅=3a₄=6，a₄=2。
（Ⅱ），a₄-a₁=3d=2+4=6所以d=2，所以数列{a_n}的通项公式即a_n=-4+(n-1)d=-4+(n-1)x2=2n-6。

填空题

1、从某工厂生产的产品中随机取出4件，测得其正常使用天数分别为27，28，30，31，则这4件产品正常使用天数的平均数为__________．

答 案：29

解 析： 【考情点拨】本题主要考查的知识点为平均数．【应试指导】 

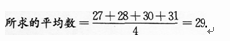
2、

答 案：-1/2