课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2022年成考高起点《数学(理)》每日一练试题08月13日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、
答 案:A
2、已知在平行六面体ABCD-A´B´C´D´中,AB=5,AD=3,AA´=6,∠BAD=∠BAA´=∠DAA´=60°,AC´=()。
答 案:A
解 析: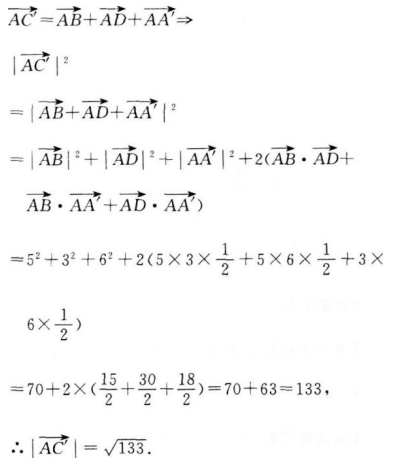
3、若函数ƒ(x)的定义域为[0,1],则ƒ(cosx)的定义域为()。
- A:[0,1]
- B:(-∞,+∞)
- C:[-π/2,π/2]
- D:[2kπ-π/2,2kπ+π/2](k∈Z)
答 案:D
解 析:求ƒ(cosx)的定义域,就是求自变量x的取值范围,由已知函数ƒ(x)的定义域为[0,1],利用已知条件,将cosx看作x,得0≤cosx≤1,2kπ-π/2≤x≤2kπ+π/2(k∈Z)。
4、已知sinα<0且tanα<0,则α是()。
- A:第一象限角
- B:第二象限角
- C:第三象限角
- D:第四象限角
答 案:D
解 析:已知正弦函数值在第三、四象限小于0,正切函数值在第二、四象限小于0,所以题中所求角在第四象限。
主观题
1、正三棱柱ABC—A'B'C',底面边长为a,侧棱长为h。
(I)求点A到△A'BC所在平面的距离d;
(Ⅱ)在满足d=1的上述正三棱柱中,求侧面积的最小值。
答 案:
2、在边长为a的正方形中作一矩形,使矩形的顶点分别在正方形的四条边上,而它的边与正方形的对角线平行,问如何作法才能使这个矩形的面积最大?
答 案: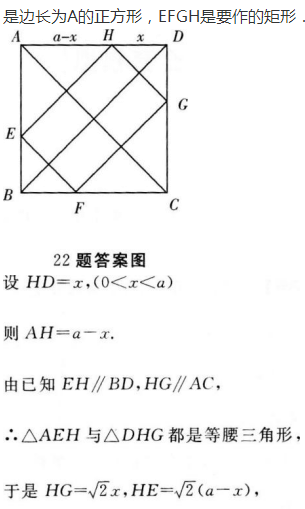

3、已知函数f(x)=2x3—3x2+2。(Ⅰ)求f'(x);
(Ⅱ)求f(x)在区间[-2,2]的最大值与最小值
答 案:(I)f'(x)=6x2—6x.(Ⅱ)令f'(x)=0,解得x=0或x=1.因为f(-2)=-26,f(0)=2,f(1)=1,f(2)=6,
所以f(x)在区间[-2,2]的最大值为6,最小值为-26。
4、在锐角二面角α-l-β中,P∈α,A、B∈l,∠APB=90°,PA=2√3,PB=2√6,PB与β成30°角,求二面角α-l-β的大小。
答 案:
填空题
1、如果二次函数的图像经过原点和点(-4,0),则该第二次函数图像的对称轴方程
答 案:x=-2
2、已知sinx= ,且x为第四象限角,则sin2x=___________________ 。
,且x为第四象限角,则sin2x=___________________ 。
答 案: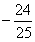
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!



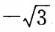
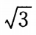
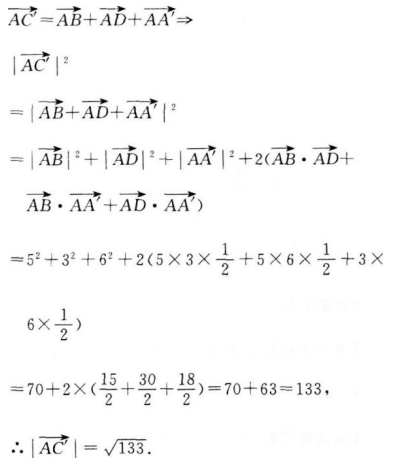




 ,且x为第四象限角,则sin2x=___________________ 。
,且x为第四象限角,则sin2x=___________________ 。