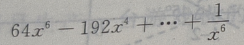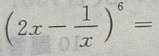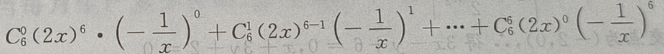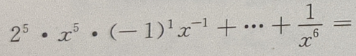2023年成考高起点《数学(理)》每日一练试题07月02日
2023-07-02 11:39:38 来源：吉格考试网
2023年成考高起点《数学(理)》每日一练试题07月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、设双曲线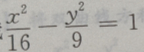
的渐近线的斜率为k，则|k|=（）
- A：
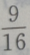
- B：
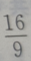
- C：
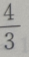
- D：
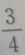
答 案：D
解 析：双曲线渐近线的斜率为k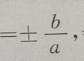
故本题中k
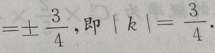
2、设0 答 案：D 解 析： 3、已知复数z=a+bi,其中a, 答 案：C 解 析：注意区分 4、参数方程 答 案：B 解 析： 主观题 1、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程； 答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得 2、建筑一个容积为8000 答 案： 3、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c． 答 案：由已知得 4、已知直线l的斜率为1，l过抛物线C： 答 案：(I）C的焦点为 填空题 1、不等式 答 案： 解 析： 2、 答 案： 解 析：
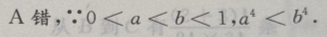
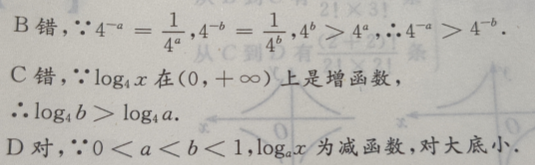
且b≠0，则（）
（
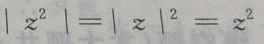
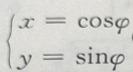为参数）表示的图形为（）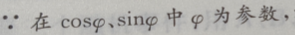
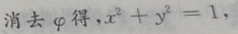即半径为1的圆，圆心在原点
(II）求f（x）的极值．
当
时，f'(x)
单调递减，在区间
单调递增．因此f(x）在
时取得极小值
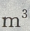,深为6m的长方体蓄水池，池壁每
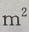的造价为15元，池底每
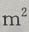的造价为30元。（I）把总造价y(元)表示为长x(m)的函数；（Ⅱ）求函数的定义域
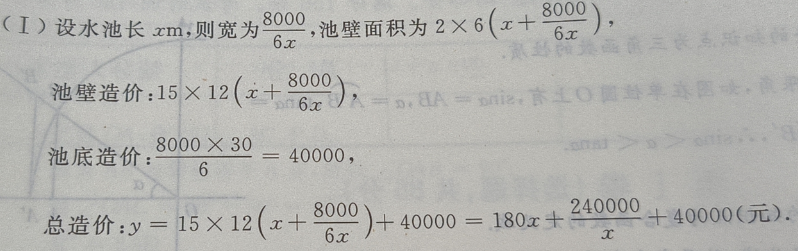
解得
的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
，得
设A（x1,y1），B（x2,y2），则
因此
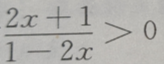的解集为（）
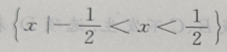
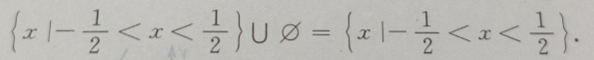
的展开式是（）
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
