2023年成考高起点《数学(理)》每日一练试题06月29日
2023-06-29 11:36:28 来源:吉格考试网
2023年成考高起点《数学(理)》每日一练试题06月29日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、 展开式中,末3项的系数(a,x 均未知) 之和为()
展开式中,末3项的系数(a,x 均未知) 之和为()
- A:22
- B:12
- C:10
- D:-10
答 案:C
解 析: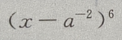

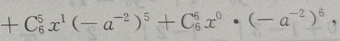 末三项数之和为
末三项数之和为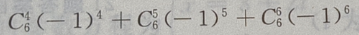
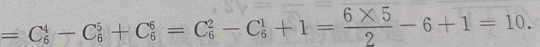
2、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 3、圆 答 案:A 解 析:因为 4、设甲: 答 案:A 解 析:三角形相似不一定全等,但三角形全等一定相似,因此,甲是乙的必要条件但不是充分条件. 主观题 1、建筑一个容积为8000 答 案: 2、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程; 答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 3、在正四棱柱ABCD-A'B'C'D'中, 答 案:(Ⅰ)由题意知(如图所示) 4、设函数f(x)= 答 案:(Ⅰ)函数的定义域为 填空题 1、函数 答 案:2 解 析:当x=0时,y= 2、设离散型随机变量 答 案:5.48 解 析: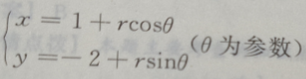 的圆心在()点上
的圆心在()点上
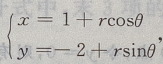 所以圆的圆心为O(1,-2)
所以圆的圆心为O(1,-2) ;乙:
;乙: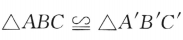 .则()
.则()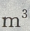 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每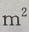 的造价为15元,池底每
的造价为15元,池底每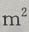 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
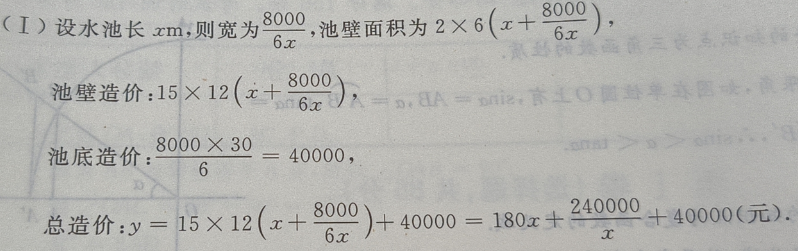

(II)求f(x)的极值. 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
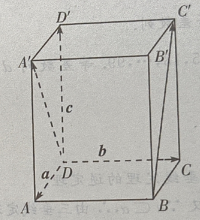
 (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
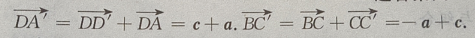
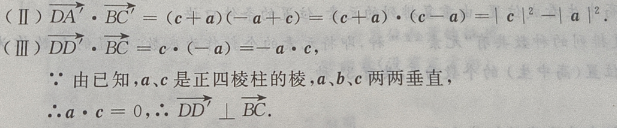
 (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值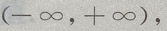
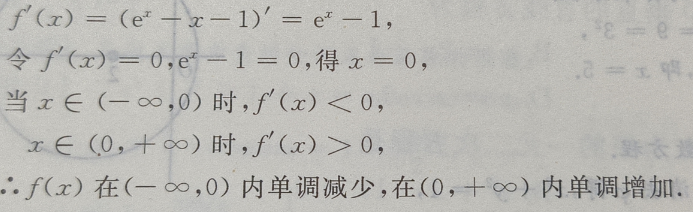 (Ⅱ)
(Ⅱ)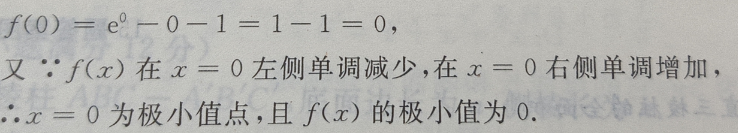
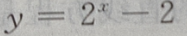 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
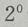 -2=-1,故函数与y轴交于(0,-1)点,令y=0,则有
-2=-1,故函数与y轴交于(0,-1)点,令y=0,则有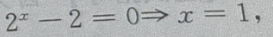 故函数与x轴交于(1,0) 点,因此函数
故函数与x轴交于(1,0) 点,因此函数 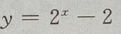 与坐标轴的交点共有 2个.
与坐标轴的交点共有 2个. 的分布列如下表,那么
的分布列如下表,那么 的期望等于()
的期望等于()

 =6×0.7+5.4×0.1+5×0.1+4×0.06+0×0.04=5.48
=6×0.7+5.4×0.1+5×0.1+4×0.06+0×0.04=5.48



