2023年成考高起点《数学(理)》每日一练试题05月10日
2023-05-10 11:22:46 来源:吉格考试网
2023年成考高起点《数学(理)》每日一练试题05月10日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设0 答 案:D 解 析: 2、给出下列两个命题:①如果一条直线与一个平面垂直,则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点,在二面角的两个面内分别作射线,则这两条射线所成的角为该二面角的平面角.则() 答 案:B 解 析:一条直线与平面垂直,则直线与平面内的任意一条直线垂直,故①为真命题;二面角的两条射线必须垂直于二面角的棱,故②为假命题,因此选B选项. 3、函数 答 案:A 解 析: 4、已知复数z=a+bi,其中a, 答 案:C 解 析:注意区分 主观题 1、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 答 案:如图, 2、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 3、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程; 答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 4、已知数列 答 案: 填空题 1、lg(tan43°tan45°tan47°)=()
答 案:0 解 析:lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0 2、设离散型随机变量 答 案:5.48 解 析:



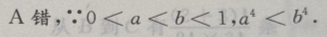
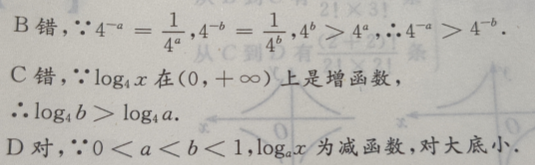
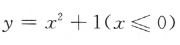 的反函数是()
的反函数是()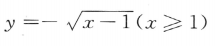
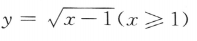
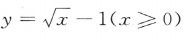

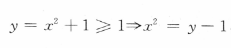 ,由于x≤0,故
,由于x≤0,故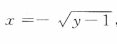 把x与y互换,得所求反函数为
把x与y互换,得所求反函数为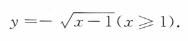
 且b≠0,则()
且b≠0,则()

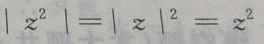




 AB=120m,求河的宽
AB=120m,求河的宽

 ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
(II)求f(x)的极值. 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。


 的分布列如下表,那么
的分布列如下表,那么 的期望等于()
的期望等于()

 =6×0.7+5.4×0.1+5×0.1+4×0.06+0×0.04=5.48
=6×0.7+5.4×0.1+5×0.1+4×0.06+0×0.04=5.48



