课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2022年成考高起点《数学(理)》每日一练试题07月20日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数y=√2sin 的最小正周期为()。
的最小正周期为()。
答 案:B
解 析: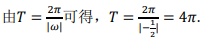
2、若函数f(x)是奇函数,则函数F(x)=f(x)*sin(3π/2-x)的奇偶性是()。
- A:奇函数
- B:偶函数
- C:非奇非偶函数
- D:既是奇函数.又是偶函数
答 案:A
解 析:∵ƒ(x)是奇函数,∴ƒ(-x)=-ƒ(x);∵F(x)=f(x)*(-cosx)=-f(x)cosx;∴F(-x)=-f(-x)cos(-x)=ƒ(x)cosx=-F(x);∴F(x)=f(x)*sin(3π/2-x)为奇函数。
3、对满足a>b的任意两个非零实数,下列不等式成立的是()。
答 案:D
4、不等式∣x-3∣>2的解集是
- A:{ x∣x >5或x <1}
- B:{ x∣x <1}
- C:{ x∣1
- D:{ x>5}
答 案:A
解 析:该小题主要考查的知识点为不等式的解集.【考试指导】∣x-3∣>2=>x-3>2或x-3<—2=>x〉5 或x〈 1.
主观题
1、
答 案:
2、在锐角二面角α-l-β中,P∈α,A、B∈l,∠APB=90°,PA=2√3,PB=2√6,PB与β成30°角,求二面角α-l-β的大小。
答 案:
3、已知函数f(x)=x3+x2-5x-1。求:(1)f(x)的单调区间; (2)f(x)零点的个数。
答 案:
4、在△ABC中,A=30°,AB= ,BC=1.(Ⅰ)求C;(Ⅱ)求△ABC的面积.
,BC=1.(Ⅰ)求C;(Ⅱ)求△ABC的面积.
答 案:
填空题
1、椭圆的中心在原点,一个顶点和一个焦点分别是直线x+3y-6=0与两坐标轴的交点,则此椭圆的标准方程为( )。
答 案:
解 析:
2、曲线y=x2-ex+1在点(0,0)处的切线方程为___________________。
答 案:x+y=0
解 析:本题考查了导数的几何意义的知识点。 根据导数的几何意义,曲线在(0,0)处的切线斜率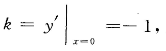 ,则切线方程为y-0=-1·(x-0),化简得:x+y=0。
,则切线方程为y-0=-1·(x-0),化简得:x+y=0。
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
 的最小正周期为()。
的最小正周期为()。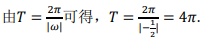
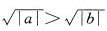

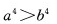
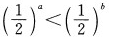




 ,BC=1.(Ⅰ)求C;(Ⅱ)求△ABC的面积.
,BC=1.(Ⅰ)求C;(Ⅱ)求△ABC的面积.


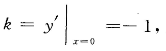 ,则切线方程为y-0=-1·(x-0),化简得:x+y=0。
,则切线方程为y-0=-1·(x-0),化简得:x+y=0。


