2022年成考高起点《数学(理)》每日一练试题07月13日

2022年成考高起点《数学(理)》每日一练试题07月13日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、根据连续函数的定义，下列函数在指定点或开区间上不连续的是（）

• A：ƒ(x)=2x+1，点x=-1
• B：ƒ(x)=ax^{2+bx+C，点x=0}
• C：
• D：

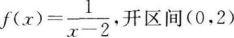
答 案：C

2、已知一次函数y＝2x＋b的图像经过点（-2，1），则该图像也经过点（　　）

• A：（1，7）
• B：（1，-3）
• C：（1，5）
• D：（1，-1）

答 案：A

解 析：因为一次函数了y＝2x＋b的图像过点（－2，1），所以，1＝2×（－2）＋b，b＝5，即y＝2x＋5．结合选项，当x＝1时，y＝7，故本题选A．

3、函数f(x)=2cos(3x-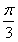)在区间[-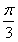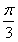，]的最大值是()。

• A：0
• B：
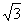
• C：2
• D：-1

答 案：C

解 析：本题考查了三角函数的最值的知识点。 当x=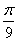时，函数f(x)=2cos(3x-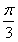)取最大值，最大值为2。

4、已知集合M={1，-2，3)，N=(-4，5，6，-7)，从这两个集合中各取一个元素作为一个点的直角坐标，其中在第一、二象限内不同的点的个数是（）。

• A：18
• B：16
• C：14
• D：10

答 案：C

主观题

1、已知椭圆C的长轴长为4，两焦点分别为F1(-，0)，F2(，0)。 (1)求C的标准方程;(2)若P为C上一点，|PF1|-|PF2|=2，求cos∠F1PF2。

答 案：

2、已知数列{an}的前n项和 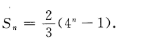(1)求{an}的通项公式; (2)若ak=128，求k。

答 案：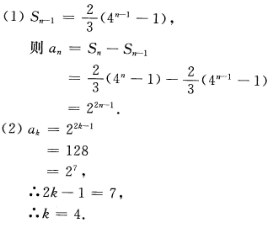

3、A、B、C是直线L上的三点，P是这条直线外一点，已知AB=BC=a，∠APB=90°，∠BPC=45°。求：(Ⅰ)∠PAB的正弦；
(Ⅱ）线段PB的长；
(Ⅲ)P点到直线L的距离

答 案：

4、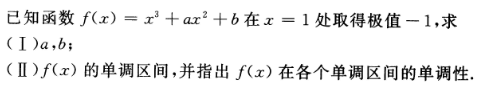

答 案：

填空题

1、曲线y=x³-2x在点（1，-1）处的切线方程为______.

答 案：y=x-2

解 析：该小题主要考查的知识点为切线方程.

2、已知曲线y=lnx+a在点(1，a)处的切线过点(2，-1)，则a=______。

答 案：-2

解 析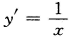：，故曲线在点(1，a)处的切线的斜率为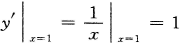，因此切线方程为：y-a=x-1，即y=x-1+a，又切线过点(2，-1)，因此有-1=2-1+a，故a=-2.