2023年成考高起点《数学(理)》每日一练试题03月11日
2023-03-11 11:18:42 来源：吉格考试网
2023年成考高起点《数学(理)》每日一练试题03月11日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、函数f(x)=tan(2x+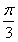
)的最小正周期是()。
- A：
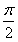
- B：2π
- C：7π
- D：4π
答 案：A
解 析：本题考查了三角函数的周期的知识点。
最小正周期
。
2、
- A：
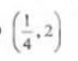
- B：
- C：
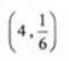
- D：
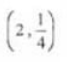
答 案：A
3、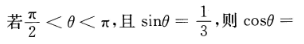
（）。
- A：
- B：
- C：
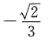
- D：
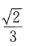
答 案：B
解 析：该小题主要考查的知识点为三角函数.【考试指导】
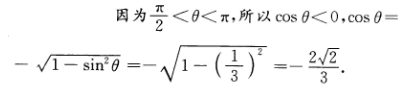
4、设0＜x＜l，则（）
- A：log2x＞0
- B：0＜2x＜1
- C：
- D：1＜2x＜2
答 案：D
解 析：当0＜x＜1时，1＜2x＜2，log2x＜0，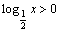
.
主观题
1、已知函数f(x)=x3+x2-5x-1。求：(1)f(x)的单调区间; (2)f(x)零点的个数。
答 案：
2、在边长为a的正方形中作一矩形，使矩形的顶点分别在正方形的四条边上，而它的边与正方形的对角线平行，问如何作法才能使这个矩形的面积最大?
答 案：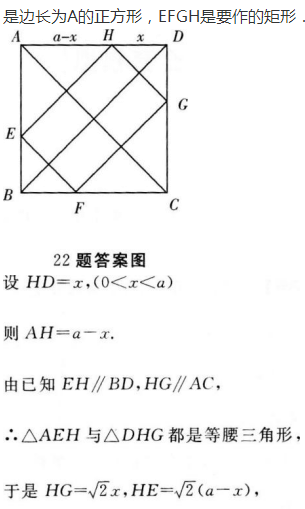
3、已知函数f(x)=2x3—3x2+2。(Ⅰ)求f'(x)；
(Ⅱ)求f(x)在区间[-2，2]的最大值与最小值
答 案：(I)f'(x)=6x2—6x．(Ⅱ)令f'(x)=0，解得x=0或x=1．因为f(-2)=-26，f(0)=2，f(1)=1，f(2)=6，
所以f(x)在区间[-2，2]的最大值为6，最小值为-26。
4、
答 案：
填空题
1、函数f(x)=x2-2x+1在x=1处的导数为______。
答 案：f’(x）=(x2-2x+1)’=2x-2，故f’(1)=2×1-2=0.
2、从一个正方体中截去四个三棱锥，得一正三棱锥ABCD，正三棱锥的体积是正方体体积的( )。
答 案：1/3
解 析：截去的四个三棱锥的体积相等，其中任一个三棱锥都是底面为直角三角形,且直角边长与这个三棱锥的高相等，都等于正方体的棱长．设正方体的棱长为a，则截去的一个三棱锥的体积为
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
