2023年成考高起点《数学(文史)》每日一练试题02月14日

2023年成考高起点《数学(文史)》每日一练试题02月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

2、函数y=sin(x+3)+sin(x-3)的最大值为（）

• A：-2sin3
• B：2sin3
• C：-2cos3
• D：2cos3

答 案：D

解 析：y=sinxcos3+cosxsin3+sinxcos3-cosxsin3=2sinxcos3，sinx的最大值为1，故原函数的最大值为2cos3.

3、已知平面向量a(-2，1)与b= (A，2)垂直，则A=

• A：4
• B：-4
• C：-1
• D：1

答 案：D

解 析：因为a与b垂直，所以a·b=-2A+2=0，A=1。

4、函数y=tan(2x+π/4)的最小正周期为（）。

• A：π
• B：
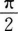
• C：
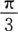
• D：2π

答 案：B

解 析：由正切函数y=tan(ωx+φ)的最

主观题

1、弹簧的伸长与下面所挂砝码的重量成正比，已知弹簧挂20g重的砝码时长度是12cm，挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度。

答 案：设弹簧原长为y0cm，则弹簧伸长量为(y-y0)cm，由题意得y-y0=kx，即y=kx+y0,

所求函数关系式为y=0.2x+8，弹簧的原长为8cm。

2、在平面直角坐标系xOy中，已知⊙M的方程为x²+y²-2x+2y-6=0，⊙O经过点M. (Ⅰ）求⊙O的方程； (Ⅱ)证明：直线x-y+2=0与⊙M，⊙O都相切.

答 案：(Ⅰ)⊙M可化为标准方程(x-1)²+(y+1)²=(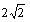)²， 其圆心M点的坐标为（1，-1)，半径为r₁=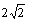， ⊙O的圆心为坐标原点， 可设其标准方程为x²+y²=r₂²， ⊙O过M点，故有r₂=， 因此⊙O的标准方程为x²+y²=2. (Ⅱ)点M到直线的距离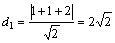， 点O到直线的距离离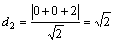， 故⊙M和⊙O的圆心到直线x-y+2=0的距离均等于其半径， 即直线x-y+2=0与⊙M和⊙O都相切.

3、(I)求E的离心率; 　　

答 案：由题设知△AF1F2为直角三角形，且 设焦距|F₁F₂|= 2c，则|AF₂|=3/2c如，|AF₁|=5/2c，2a=|AF₁|+|AF₂|= 4c. 所以离心率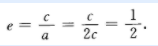

4、椭圆的焦点F1(-1，0)，F2(1，0)，｜F1F2｜是｜PF1｜和｜PF2｜的等差中项。
(Ⅰ)求椭圆方程；
(Ⅱ)若∠F2F1P=120°，求△PF1F2的面积。

答 案：
(Ⅱ)如图，设P点的横坐标为-1-m(m>0)，

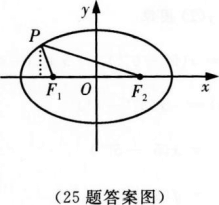
填空题

1、已知sinα-cosα=a，计算sinαcosα=（）。

答 案：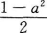

解 析：∵sinα-cosα=a，∴(sinα-cosα)2=a2，

2、拋物线y²= 2px的准线过双曲线x²/3-y²=1的左焦点，则p=

答 案：由题意知，p>抛物线y^2??= 2px的准线为x=-p/2，双曲线x^2??/3-y^2??=1的左焦点为 ，即(-2,0)，由题意知，-p/2 =-2,p =4