2023年成考高起点《数学(理)》每日一练试题01月30日

2023年成考高起点《数学(理)》每日一练试题01月30日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、甲、乙各进行一次射击，若甲击中目标的概率是0．4，乙击中目标的概率是0．5，且甲、乙是否击中目标相互独立，则甲、乙都击中目标的概率是（）。

• A：0.9
• B：0.5
• C：0.4
• D：0.2

答 案：D

解 析：甲、乙都击中目标的概率为0.4×0.5=0.2。

2、下列函数中，为偶函数的是（）。  

• A：y=log₂x
• B：y=x²
• C：y=4/x
• D：y=x²+x

答 案：B

解 析：该小题主要考查的知识点为偶函数的性质. 【考试指导】

3、函数y=log₂(x+l)的定义域是（）

• A：(2，+∞）
• B：(-2，+∞)
• C：(-∞，-1)
• D：(-1，+∞)

答 案：D

解 析：由对数函数的性质可知x+l＞0=>x＞-1，故函数的定义域为（-1，+∞).

4、不等式x²-2x-3＜0的解集为（）。

• A：(-1,3)
• B：(1,3)
• C：(-3,1)
• D：(1/3,1)

答 案：A

解 析：x²-2x-3＜0，(x+1)(x-3)＜0，x∈(-1,3)。

主观题

1、
(I)求C的标准方程；
(Ⅱ)设P为C的左顶点，求△PMN的面积

答 案：(I)(Ⅱ)

2、已知{an}是等差数列，且a2=-2，a4=-1. (Ⅰ)求{an}的通项公式； (Ⅱ)求{an}的前n项和Sn.

答 案：

3、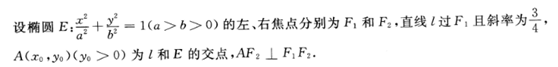(Ⅰ)求E的离心率；(Ⅱ)若E的焦距为2,求其方程.

答 案：

4、在△ABC中，AB=2,BC=3,B=60°，求AC及△ABC的面积。

答 案：根据余弦定理得出

填空题

1、设离散型随机变量ξ的分布列如下表。那么ξ的期望等于（）。

答 案：5.48

解 析：E(ξ)=6×0.7+5.4×0.1+5×0.1+4×0.06+0×0.04=5.48。

2、设离散型随机变量ζ的分布列如下表所示，那么ζ的期望等于（）。

答 案：89

解 析：E(ξ)=100x0.2+90x0.5+80x0.3=89。