2023年成考高起点《数学(理)》每日一练试题01月10日

2023年成考高起点《数学(理)》每日一练试题01月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数y=log₂(x+l)的定义域是（）

• A：(2，+∞）
• B：(-2，+∞)
• C：(-∞，-1)
• D：(-1，+∞)

答 案：D

解 析：由对数函数的性质可知x+l＞0=>x＞-1，故函数的定义域为（-1，+∞).

2、已知平面α，两条直线l1，l2。设甲：l1⊥α且l2⊥α；
乙：l1//l2，
则（）。

• A：甲是乙的必要条件但不是充分条件
• B：甲是乙的充分条件但不是必要条件
• C：甲是乙的充要条件
• D：甲既不是乙的充分条件也不是乙的必要条件

答 案：B

解 析：如果两直线垂直于同一平面，则两直线平行；但是如果两直线平行，这两条直线不一定垂直于同一平面，也可能两直线是在平面内，所以甲是乙的充分条件但不是必要条件，选择B。

3、

• A：
• B：[0,2]
• C：[-2,2]
• D：

答 案：C

4、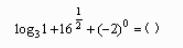

• A：2
• B：4
• C：3
• D：5

答 案：D

主观题

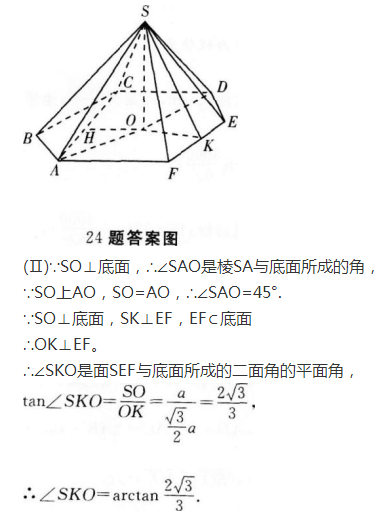
1、正三棱柱ABC—A'B'C'，底面边长为a，侧棱长为h。
(I)求点A到△A'BC所在平面的距离d；
(Ⅱ)在满足d=1的上述正三棱柱中，求侧面积的最小值。

答 案：

2、

答 案：

3、建筑一个容积为8000m³，深为6m的长方体蓄水池，池壁每m²的造价为15元，池底每m²的造价为30元。(Ⅰ)把总造价y(元)表示为长x(m)的函数；
(Ⅱ)求函数的定义域。

答 案：

4、已知A，B为⊙O上的两点，且AB=33，∠ABO=30°，求⊙O的半径。

答 案：设⊙O的半径为r，则OA=OB=r。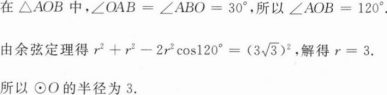

填空题

1、设离散型随机变量ζ的分布列如下表所示，那么ζ的期望等于（）。

答 案：89

解 析：E(ξ)=100x0.2+90x0.5+80x0.3=89。

2、曲线y=x²-e^x+1在点(0，0)处的切线方程为___________________。

答 案：x+y=0  

解 析：本题考查了导数的几何意义的知识点。 根据导数的几何意义，曲线在(0，0)处的切线斜率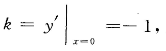，则切线方程为y-0=-1·(x-0)，化简得：x+y=0。