2022年成考高起点《数学(理)》每日一练试题07月02日

2022年成考高起点《数学(理)》每日一练试题07月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、下列函数中，为减函数的是 （ ）

• A：y=x³
• B：y=sinx
• C：y=-x³
• D：y=cosx

答 案：C

解 析：本题主要考查的知识点为函数的增减性．  【应试指导】易知三角函数y=sinx，y=COSX在R上为不增不减函数，函数y=x在R上为增函数，y=-x2在R上为减函数．

2、若直线l与平面M平行，则在平面M内与l垂直的直线

• A：有无数条
• B：只有一条
• C：只有两条
• D：不存在

答 案：D

3、不等式x²-2x-3＜0的解集为（）。

• A：(-1,3)
• B：(1,3)
• C：(-3,1)
• D：(1/3,1)

答 案：A

解 析：x²-2x-3＜0，(x+1)(x-3)＜0，x∈(-1,3)。

4、若1名女生和3名男生随机地站成一列，则从前面数第2名是女生的概率为（）。

• A：1/4
• B：1/3
• C：1/2
• D：3/4

答 案：A

解 析：该小题主要考查的知识点为随机事件的概率. 【考试指导】设A表示第2名是女生，P(A)=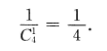

主观题

1、设函数f(x)=x3+x-1.(Ⅰ)求f(x)的单调区间；(Ⅱ)求出一个区间(a，b)，使得f(x)在区间（a，b)存在零点，且b-a＜0.5.

答 案：(Ⅰ)f’(x)=3x²+1＞0， 故函数在R上单调递增，故其单调区间为R.

2、在平面直角坐标系xOy中，已知⊙M的方程为x2+y2-2x+2y-6=0，⊙O经过点M. (Ⅰ）求⊙O的方程； (Ⅱ)证明：直线x-y+2=0与⊙M，⊙O都相切.

答 案：(Ⅰ)⊙M可化为标准方程(x-1)²+(y+1)²=(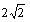)²， 其圆心M点的坐标为（1，-1)，半径为r₁=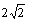， ⊙O的圆心为坐标原点， 可设其标准方程为x²+y²=r₂²， ⊙O过M点，故有r₂=， 因此⊙O的标准方程为x²+y²=2. (Ⅱ)点M到直线的距离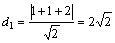， 点O到直线的距离离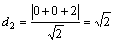， 故⊙M和⊙O的圆心到直线x-y+2=0的距离均等于其半径， 即直线x-y+2=0与⊙M和⊙O都相切.

3、已知{an}为等差数列，且a3=a5+1. (Ⅰ)求{an}的公差d； (Ⅱ)若a1=2，求{an}的前20项和S20.

答 案：(Ⅰ)设公差为d，知a₅=a+₃2d， 故a₅=a₃+2d=a₃-1， 因此有d=-1/2. (Ⅱ)由前n项和公式可得

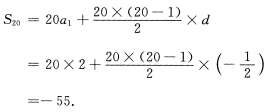
4、在△ABC中，已知B=75°，(Ⅰ)求cosA；(Ⅱ)若BC=3，求AB.

答 案：

填空题

1、设球的表面积为4π，则该球的体积为（）。

答 案：4π/3

解 析：

2、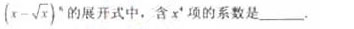

答 案：15