2023年成考高起点《数学(文史)》每日一练试题01月04日

2023年成考高起点《数学(文史)》每日一练试题01月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

2、已知函数f(x)=ax³.若f'(3)=9，则a=（）。

• A：
• B：
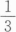
• C：1
• D：3

答 案：B

解 析：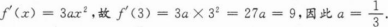

3、函数y=3sin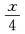

• A：8π
• B：4π
• C：2π
• D：2π/3

答 案：A

解 析：

4、若圆x²+y²=c与直线x+y=1相切，则c=（）

• A：1/2
• B：1
• C：2
• D：4

答 案：A

解 析：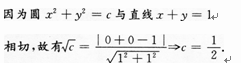         

主观题

1、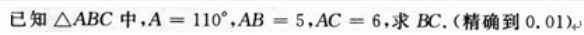

答 案：根据余弦定理， 

2、已知抛物线经过点(2，3)，对称轴方程为x=1，且在x轴上截得的弦长为4，试求抛物线的解析式。

答 案：设抛物线y=a(x-x1)(x-x2)，与x轴的两交点为A(x1，0)，B(x2，0)，由｜AB｜=4，对称轴为x=1得x1=1-2=-1，x2=1+2=3，∴y=a(x+1)(x-3)，又∵抛物线过点(2，3)，∴3=a(2+1)(2-3)，得a=-1，故所求的抛物线方程为y=-(x+1)(x-3)，即y=-x²+2x+3。

3、已知椭圆
（Ⅰ）求C的方程；
（Ⅱ）设C上一点P的横坐标为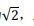F₁、F₂为C的左、右焦点，求△PF₁F₂的面积。

答 案：（Ⅰ）由等比数列的性质可知：a²b²=18；离心率为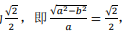得a²=6，b²=3，所以C的方程为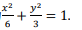
（Ⅱ）

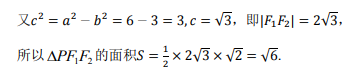
4、已知椭圆C的长轴长为4，两焦点分别为F1(-，0)，F2(，0)。 (1)求C的标准方程;(2)若P为C上一点，|PF1|-|PF2|=2，求cos∠F1PF2。

答 案：

填空题

1、任选一个不大于20的正整数，它恰好是3的整数倍的概率是（）。

答 案：3/10

解 析：设n为不大于20的正整数的个数，则n=20，m为在这20个数中3的倍数：3、6、9、12、15、18的个数，所以m=6，所求的概率为m/n=6/20=3/10。

2、某小组有11名学生，其中女生4名，现选举2人当代表，要求至少有一名女生当选，则不同的选法有（）种。

答 案：34

解 析：