2022年成考高起点《数学(文史)》每日一练试题12月31日

2022年成考高起点《数学(文史)》每日一练试题12月31日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

2、

• A：
• B：
• C：
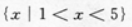
• D：

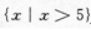
答 案：A

解 析：本题主要考查的知识点为不等式的解集．  【应试指导】           

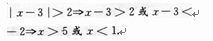
3、已知点A(1，0)，B(-1，1)，若直线kx-y-1=0与直线AB平行，则k=（）

• A：
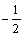
• B：
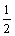
• C：-1
• D：1

答 案：A

解 析：两直线平行则其斜率相等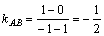，，而直线kx-7-1=0的斜率为k，故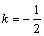

4、从甲口袋内摸出一个球是红球的概率是0.2，从乙口袋内摸出一个球是红球的概率是0.3，现从甲、乙两个口袋内各摸出一个球，这两个球都是红球的概率是

• A：0.94
• B：0.56
• C：0.38
• D：0.06

答 案：D

主观题

1、设S_n为数列{a_n}的前n项和，S_n=3/2(a_n-1)(n∈N₊)，数列{b_n}的通项公式为b_n=4n+3(n∈N₊)。
(Ⅰ)求数列｛an｝的通项公式；
(Ⅱ)若di∈{a1，a2，…，an，…}∩{b1，b2，…，bn，…}(i=1，2，…，n，…)，则称数列{dn}为数列{an}与{bn}的公共项，将数列{an}与{bn}的公共项按它们在原数列中的先后顺序排成一个新的数列(dn)，证明{dn}的通项公式为dn=3²ⁿ⁺¹(n∈N)。

答 案：

2、已知数列 {a_n}中，S_n是它的前n项和，并且 S_n+1=4a_n+2，a1=1。（Ⅰ）设 b_n=a_n+1−2a_n，求证：数列{b_n}是等比数列；
（Ⅱ）设 c_n=a_n/2ⁿ，求证：数列{c_n}是等差数列；
（Ⅲ）求数列{a_n}的通项公式及前n项和。

答 案：

3、设ƒ(x)=a^x-1，其中常数a>0，如果{xn}是等差数列，且x_n=2n-1，
(Ⅰ)求证：{ƒ(xn)}是等比数列；
(Ⅱ)求数列{ƒ(xn)}的前n项和Sn的表达式。

答 案：

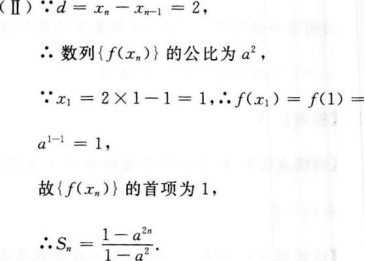
4、从某公司生产的安全带中随机抽取10条进行断力测试，测试结果（单位：kg）
如下：
3722 3872 4004 4012 3972 3778
4022 4006 3986 4026
则该样本的样本方差为______kg（精确到0.1）

答 案：10928.8

解 析：10928.8

填空题

1、某小组有11名学生，其中女生4名，现选举2人当代表，要求至少有一名女生当选，则不同的选法有（）种。

答 案：34

解 析：

2、已知平面向量a=(1,2)，b=(-2,3),2a+3b=

答 案：（-4,13）

解 析：2a+2b=2(1,2)+3(-2,3)=（-4,13）