2022年成考高起点《数学(理)》每日一练试题12月27日
2022-12-27 11:11:01 来源:吉格考试网
2022年成考高起点《数学(理)》每日一练试题12月27日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设a,b,c为实数,则()。
- A:a - c>b –c
- B:|a|>|b|
- C:

- D:ac>bc
答 案:A
解 析:该小题主要考查的知识点为不等式的性质. 【考试指导】a>b,则a-c>b—c.
2、曲线y=x3-4x+2在点(1,-1)处的切线方程为( )
- A:x-y-2=0
- B:x-y=0
- C:x+y=0
- D:x+y-2=0
答 案:C
解 析: ,因此,曲线在点(1,-1)处的切线方程应该为:y+1=-1(x-1),也就是x+y=0.答案为:C
,因此,曲线在点(1,-1)处的切线方程应该为:y+1=-1(x-1),也就是x+y=0.答案为:C
3、等差数列{an}中,若a1=2,a3=6,则a7=()。
- A:10
- B:12
- C:14
- D:8
答 案:C
解 析:该小题主要考查的知识点为等差数列的性质.【考试指导】
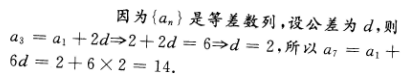
4、已知偶函数y=ƒ(x)在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=ƒ(x)在区间[a,b](0 主观题 1、已知数列{an}的前n项和 答 案: 2、正四面体ABCD内接于半径为R的球,求正四面体的棱长。
答 案: 3、已知椭圆C的长轴长为4,两焦点分别为F1(- 答 案: 4、某运动员射击10次,成绩(单位:环)如下 答 案: 填空题 1、圆x2+y2=5在点(1,2)处的切线的方程为()。 答 案:x+2y一5=0 解 析: 2、己知球的一个小圆的面积为π,球心到小圆所在平面的距离为 答 案:12π 解 析:
∴ƒ(-a)<ƒ(-b),即,ƒ(-b)>ƒ(-a),
∴ƒ(x)在[-b,-a]上为减函数。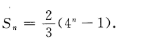 (1)求{an}的通项公式; (2)若ak=128,求k。
(1)求{an}的通项公式; (2)若ak=128,求k。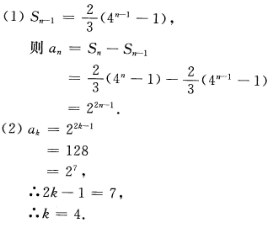

 ,0),F2(
,0),F2( ,0)。 (1)求C的标准方程;(2)若P为C上一点,|PF1|-|PF2|=2,求cos∠F1PF2。
,0)。 (1)求C的标准方程;(2)若P为C上一点,|PF1|-|PF2|=2,求cos∠F1PF2。
8、10、9、9、10、8、9、9、8、7
则该运动员的平均成绩是___________环.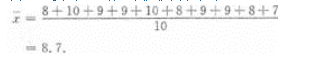

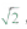 ,则这个球的表面积为()。
,则这个球的表面积为()。




