2022年成考高起点《数学(理)》每日一练试题12月09日

2022年成考高起点《数学(理)》每日一练试题12月09日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数f(x)=1+cosx的最小正周期是

• A：
• B：π
• C：
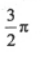
• D：2π

答 案：D

2、若p：x=1；q：x²-1=0，则（）

• A：p既不是q的充分条件也不是q的必要条件
• B：p是q的充要条件
• C：p是q的必要条件但不是充分条件
• D：p是q的充分条件但不是必要条件

答 案：D

解 析：x=1=>x²-1=0，而x²-1=0=>x=1或x=-1，故p是q的充分但不必要条件.

3、用0，1，2，3这四个数字，组成的没有重复数字的四位数共有

• A：24
• B：18
• C：12
• D：10

答 案：B

4、当圆锥的侧面积和底面积的比值是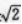时，圆锥轴截面的顶角是（ ）

• A：45°
• B：60°
• C：90°
• D：120°

答 案：C

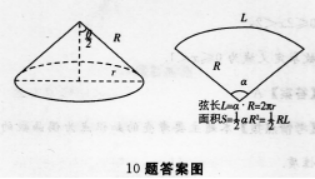
解 析：求圆锥的轴截面的顶角，先画出轴截面(如下图)，可知轴截面为等腰三角形，圆锥嘲面是扇形，固锥底面的周长等于展开侧面的扇形的孤长．

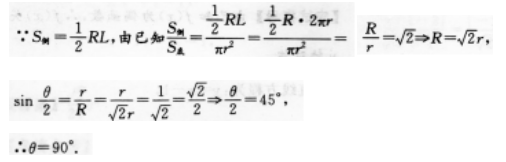
主观题

1、在△ABC中，A=30°，AB=，BC=1.(Ⅰ)求C；(Ⅱ)求△ABC的面积.

答 案：

2、某县位于沙漠边缘，到1999年底全县绿化率已达30％.从2000年开始，每年出现这样的局面：原有沙漠面积的16％被栽上树改为绿洲，而同时原有绿地面积的4％又被侵蚀，变为沙漠。(Ⅰ)设全县的面积为1,1999年底绿洲面积为a1=3/10，经过一年绿洲面积为a2，经过n年绿洲面积为an，求证：an+1=4/5an+4/25；
(Ⅱ)问至少经过多少年的绿化，才能使全县的绿洲面积超过60％(年取整数)。

答 案：

3、在△ABC中，AB=2,BC=3,B=60°，求AC及△ABC的面积。

答 案：根据余弦定理得出

4、等差数列{a_n}中，a₁=-393，a₂+a₃=-768，{b_n}是等比数列，q∈(0,1)，b1=2，{b_n}的前n项和为20，求：（Ⅰ）求a_n，b_n；
（Ⅱ）解不等式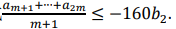

答 案：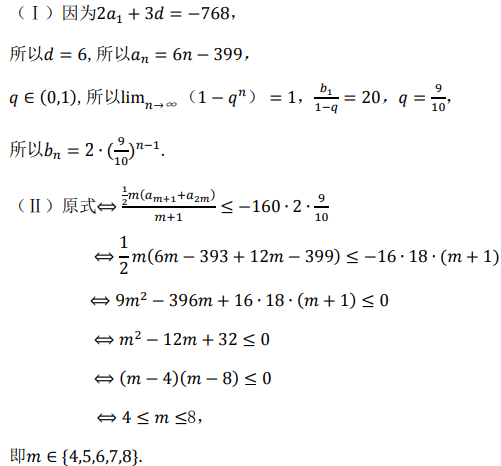

填空题

1、过圆x²+y²=25上一点M（-3，4）作该圆的切线，则此切线方程为

答 案：3x-4y+25=0

2、若向量a=(2，1,-2)，b=(-1，2,2)，则cos(a,b)=________

答 案：