2022年成考高起点《数学(理)》每日一练试题12月06日
2022-12-06 11:07:54 来源：吉格考试网
2022年成考高起点《数学(理)》每日一练试题12月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、函数y=x+1与
图像的交点个数为
- A：0
- B：1
- C：2
- D：3
答 案：C
2、函数y=（x-1）2-4，（x≥1）的反函数为
- A：
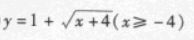
- B：
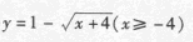
- C：
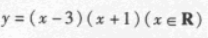
- D：
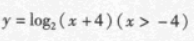
答 案：A
3、已知点A（-5，3），B（3，1），则线段AB中点的坐标为
- A：(4, -1)
- B：(-4,1)
- C：(-2,4)
- D：(-1,2)
答 案：D
4、不等式|x-2|＜1的解集是（）
- A：{x|-1＜x＜3}
- B：{x|-2＜x＜l}
- C：{x|-3＜x＜1}
- D：{x|1＜x＜3}
答 案：D
解 析：|x-2|＜1=>-1＜x-2＜1=>1＜x＜3，故不等式的解集为{x|1＜1＜3}.
主观题
1、已知等差数列前n项和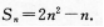
(Ⅰ)求这个数列的逋项公式；
(II)求数列第六项到第十项的和．
答 案：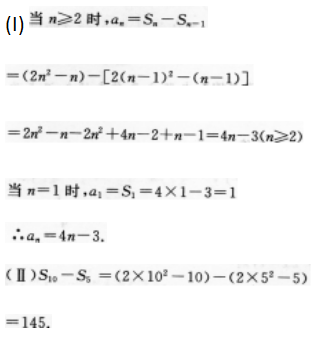
2、设椭圆的焦点为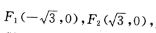
其轴长为4(Ⅰ)求椭圆的方程；(Ⅱ)设直线
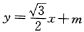与椭圆有两个不同的交点，其中一个交点的坐标是（0,1），求另一个交点的坐标。
答 案：
3、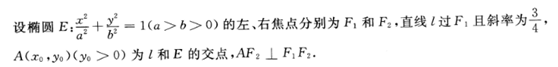
(Ⅰ)求E的离心率；(Ⅱ)若E的焦距为2,求其方程.
答 案：
4、某运动员射击10次，成绩（单位：环）如下
8、10、9、9、10、8、9、9、8、7
则该运动员的平均成绩是___________环．
答 案：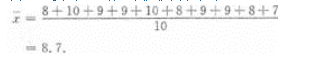
填空题
1、已知A(-1,-1)，B(3,7)两点，则线段AB的垂直平分线方程为（）。
答 案：x+2y-7=0
解 析：设线段的垂直平分线上任一点为P(x,y)，则|PA|=|PB|，即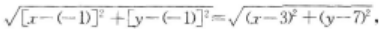
，整理得x+2y-7=0。
2、设离散型随机变量ζ的分布列如下表所示，那么ζ的期望等于（）。
答 案：89
解 析：E(ξ)=100x0.2+90x0.5+80x0.3=89。
温馨提示：因考试政策、内容不断变化与调整，本站提供的以上信息仅供参考，如有异议，请考生以权威部门公布的内容为准！
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
热门资讯
相关试卷
猜你喜欢
换一换
成人高考加分条件有哪些 成考怎么进行加分
01-26
2025年初、中级会计资格证考试时间安排
12-17
江西高职单招2025公告
12-11
江西高职单招考试时间2025
12-11
江西2025年高职单招报名时间及入口
12-11
河北省教育厅发布2025年高职单招工作的通知
12-10
江西省2025年高职单招实行文化素质全省统考+职业技能（或职业适应性）校考模式
12-09
四川省教育厅发布2025年高职单招工作通知
12-09
