2022年成考高起点《数学(文史)》每日一练试题11月28日
2022-11-28 11:15:41 来源:吉格考试网
2022年成考高起点《数学(文史)》每日一练试题11月28日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共有 ( )
- A:7种
- B:4种
- C:5种
- D:6种
答 案:C
2、已知函数f(x)的定义域为R,且f(2x)=4x+1,则f(1)=()
- A:9
- B:5
- C:7
- D:3
答 案:D
解 析: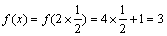
3、函数f(x)=2sin(3x+π)+1的最大值为 ( )
- A:-1
- B:1
- C:2
- D:3
答 案:D
解 析:本题主要考查的知识点为三角函数的最值. 【应试指导】

4、设f(x)为偶函数,若f(-2)=3,则f(2)=
- A:6
- B:-3
- C:0
- D:3
答 案:D
主观题
1、已知等差数列{an}中,a3+a4+a5=6。
(Ⅰ)求a4的值;
(Ⅱ)若a1=-4,求{an}的通项公式。
答 案:(Ⅰ)由等差数列的基本性质,a3+a4+a5=3a4=6,a4=2。
(Ⅱ),a4-a1=3d=2+4=6所以d=2,所以数列{an}的通项公式即an=-4+(n-1)d=-4+(n-1)x2=2n-6。
2、设函数f(x)=x3+x-1.(Ⅰ)求f(x)的单调区间;(Ⅱ)求出一个区间(a,b),使得f(x)在区间(a,b)存在零点,且b-a<0.5.
答 案:(Ⅰ)f’(x)=3x2+1>0,
故函数在R上单调递增,故其单调区间为R.

3、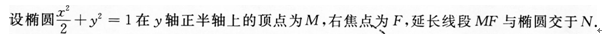 (I)求直线MF的方程;
(I)求直线MF的方程; 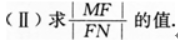
答 案:
4、已知{an}为等差数列,且a3=a5+1. (Ⅰ)求{an}的公差d; (Ⅱ)若a1=2,求{an}的前20项和S20.
答 案:(Ⅰ)设公差为d,知a5=a+32d,
故a5=a3+2d=a3-1,
因此有d=-1/2.
(Ⅱ)由前n项和公式可得
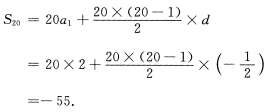
填空题
1、从某篮球运动员全年参加的比赛中任选五场,他在这五场比赛中的得分分别为21,19,15,25,20,则这个样本的方差为___________.
答 案:10.4
解 析:【考情点拨】本题主要考查的知识点为样本方差.【应试指导】样本均值为
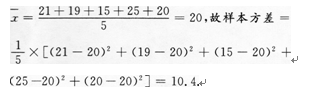
2、若28,37,x,30四个数的平均数为35,则x=()。
答 案:45
解 析: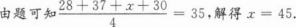
2023年成考高起点《数学(文史)》每日一练试题11月28日 11-28 2022年成考高起点《数学(文史)》每日一练试题09月28日 09-28 2022年成考高起点《数学(文史)》每日一练试题10月28日 10-28 2022年成考高起点《数学(文史)》每日一练试题08月28日 08-28 2022年成考高起点《数学(文史)》每日一练试题07月28日 07-28 2022年成考高起点《数学(文史)》每日一练试题12月28日 12-28 2022年成考高起点《数学(文史)》每日一练试题11月11日 11-11 2022年成考高起点《数学(文史)》每日一练试题07月11日 07-11



