课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2025年成考高起点《数学(理)》每日一练试题02月22日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、双曲线的渐近线方程为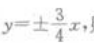 则该双曲线的离心率为()。
则该双曲线的离心率为()。
答 案:C
解 析: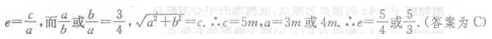
2、设甲: ;乙:
;乙: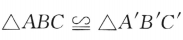 .则()
.则()
- A:甲是乙的必要条件但不是充分条件
- B:甲是乙的充分条件但不是必要条件
- C:甲是乙的充要条件
- D:甲既不是乙的充分条件也不是乙的必要条件
答 案:A
解 析:三角形相似不一定全等,但三角形全等一定相似,因此,甲是乙的必要条件但不是充分条件.
3、袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则其中恰有1个红球的概率为()
答 案:A
解 析: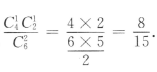
4、设F1,F2分别是椭圆的焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1,的面积等于()。
答 案:B
解 析:
主观题
1、已知设△ABC的三边长为a、b、C,2sin2A=3(sin2B+sin2C)且cos2A+3cosA+3cos(B-C)=1,求证:a:b:c= :1:1。
:1:1。
答 案:因所证的是△ABC三边的比,所以可将题中角的关系式转化为边的关系式,需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin2A=3(sin2B+sin2C)…① 由正弦定理得,2a2=3(b2+c2)…②
∵cos2A+3cosA+3cos(B-C)=1
∴3[cosA+cos(B-C)]=1-cos2A.
∵A=180°-(B+C)
∴3[-cos(B+C)+cos(B-C)]=2sin2A.
由两角和与差的余弦公式得
6sinBsinB=2sin2A…③
由①③得,2sinBsinC=sin2B+sin2C.
sin2B-2sinBsinC+sin2C=0
(sinB-sinC)2=0
sinB= sinC.
由正弦定理得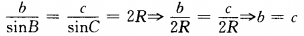
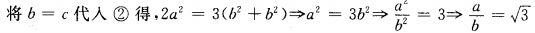
∴a:b=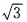 :1
:1
于是a:b:c=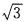 :1:1。
:1:1。
2、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 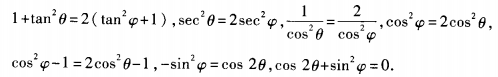
3、已知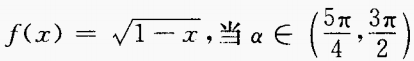 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得,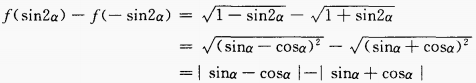
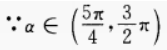 ∴sinα
∴sinα
4、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
填空题
1、曲线y=在点(1,1)处的切线方程是______。
答 案:2x+y-3=0
解 析:本题主要考查的知识点为切线方程
由题意,该切线斜率,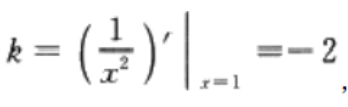 又过点(1,1),所以切线方程为y-1=-2(x-1)
又过点(1,1),所以切线方程为y-1=-2(x-1)
2、y=lg(sinx)的定义域是______。
答 案:2kπ<x<(2k+1)π(k∈Z)
解 析:sinx>0∴x属于第一、二象限,所以 2kπ<x<(2k+1)π(k∈Z)
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
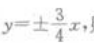 则该双曲线的离心率为()。
则该双曲线的离心率为()。
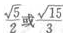
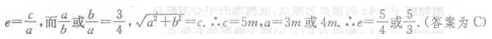
 ;乙:
;乙: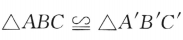 .则()
.则()
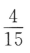

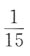
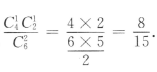
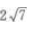
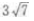
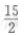

 :1:1。
:1:1。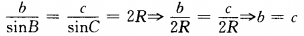
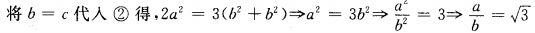
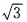 :1
:1 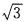 :1:1。
:1:1。
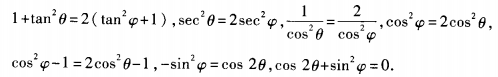
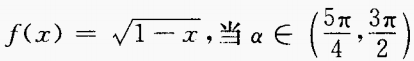 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。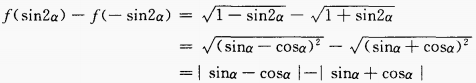
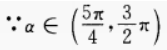 ∴sinα
∴sinα ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。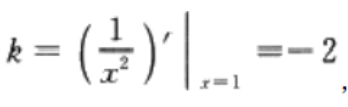 又过点(1,1),所以切线方程为y-1=-2(x-1)
又过点(1,1),所以切线方程为y-1=-2(x-1)


