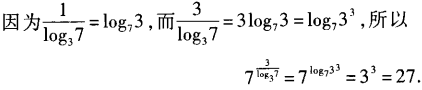课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2025年成考高起点《数学(文史)》每日一练试题01月11日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数y=2x3+3x2-12x+1在区间(-2,1)内是( )
答 案:B
解 析:y´=6x2+6x-12,在区间(-2,1)内y´<0,所以函数在区间(-2,1)内是单调递减的.
【考点指要】本题主要考查利用导数讨论函数的单调性问题,考试大纲要求会用这种方法讨论函数的性质.
2、如果点(2,一4)在一个反比例函数的图像上,那么下列四个点中也在该图像上的是()
- A:(一2,4)
- B:(一4,一2)
- C:(一2,一4)
- D:(2,4)
答 案:A
解 析:设反比例函数为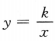 ,点(2,-4)在反比例函数的图像上,因此有
,点(2,-4)在反比例函数的图像上,因此有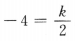 ,解得k=-8,故反比例函数
,解得k=-8,故反比例函数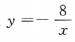 ,当x=-2时,y=4,故选A在该图像上.
,当x=-2时,y=4,故选A在该图像上.
3、b=0是直线y=kx+b过原点的()
- A:充分但不必要条件
- B:必要但不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:C
解 析:b=0 直线y=kx+b过原点
直线y=kx+b过原点
4、若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
答 案:C
解 析: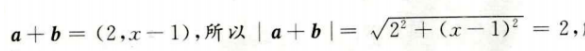 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。
主观题
1、教室里有50人在开会,其中学生35人,家长12人,老师3人,现校长在门外听到有人在发言,那么发言人是老师或学生的概率为多少?
答 案:此题属于互斥事件,发言人是老师的概率为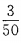 ,是学生的概率为
,是学生的概率为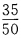 ,故所求概率为。
,故所求概率为。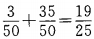
2、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35° 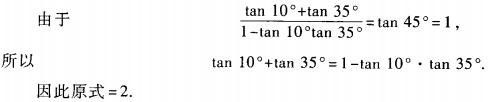
3、设函数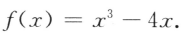
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.
答 案:(I)因为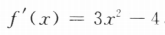 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.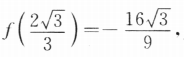 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为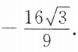
4、设3a=5b=15,求a-1+b-1的值。
答 案:由3a=15,得a=log315;又由5b=15,得b=log515。 因此a-1+b-1=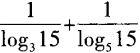 =log153+log155=1。
=log153+log155=1。
解 析:过程中应用了换底公式的推论,即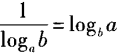
填空题
1、在△ABC中,已知AB=3,BC=5,AC=7,则cosB=______。
答 案: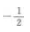
2、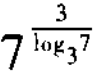 =______。
=______。
答 案:27
解 析: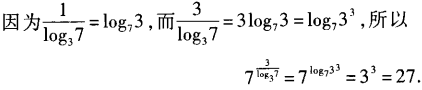
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
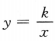 ,点(2,-4)在反比例函数的图像上,因此有
,点(2,-4)在反比例函数的图像上,因此有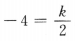 ,解得k=-8,故反比例函数
,解得k=-8,故反比例函数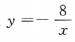 ,当x=-2时,y=4,故选A在该图像上.
,当x=-2时,y=4,故选A在该图像上. 直线y=kx+b过原点
直线y=kx+b过原点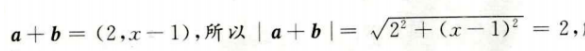 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。 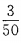 ,是学生的概率为
,是学生的概率为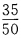 ,故所求概率为。
,故所求概率为。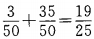
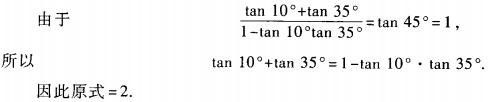
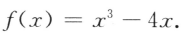
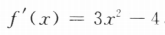 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.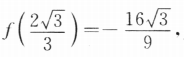 f(2)=0.
f(2)=0.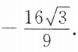
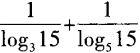 =log153+log155=1。
=log153+log155=1。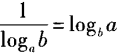
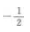
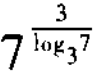 =______。
=______。