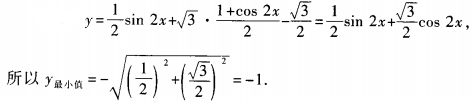2024年成考高起点《数学(理)》每日一练试题12月15日
2024-12-15 12:35:57 来源：吉格考试网
2024年成考高起点《数学(理)》每日一练试题12月15日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、设F1,F2分别是椭圆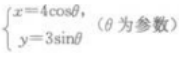
焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1的面积等于（）。
- A：
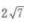
- B：
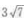
- C：
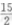
- D：2
答 案：B
解 析：消去参数,将参数方程化为普通方程,F1F2分别是椭圆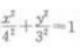
的焦点。
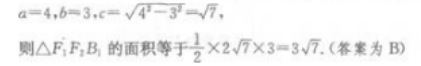
2、过A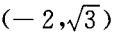
B（-5，0）两点直线的倾斜角为（）。
- A：
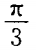
- B：
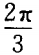
- C：
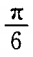
- D：
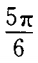
答 案：C
解 析：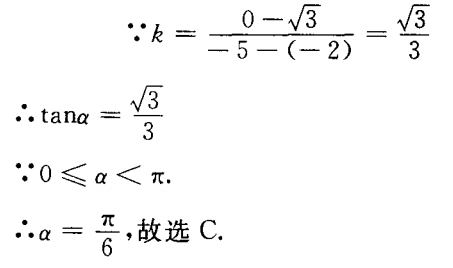
3、i为虚数单位，则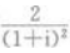
的值为（）。
- A：1
- B：－1
- C：i
- D：－i
答 案：D
解 析：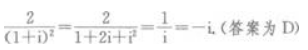
4、已知a=（-1，3），b=（-2，3），c=（0，-1），则（a·b）·c=（）。
- A：（0，-11）
- B：（11，-1）
- C：10
- D：-10
答 案：A
解 析：（a·b）·c=（-1,3）·（-2.3）·（0.-1）=（2+9）·（0，-1）=11×（0，-1）=（0，-11），故应选A。 注:向量的和、差，数乘向量结果仍为向量，向量的积为数量，掌握这些结果在解选择题时可直接用排除法，会加快解题的速度以及提高解题的准确率。
主观题
1、已知空间四边形OABC，OB=OC且∠AOB=∠AOC=θ（如图）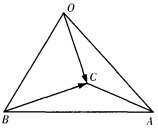
。求证：OA⊥BC。
答 案：
2、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．
答 案：由已知得
解得
3、cos20°cos40°cos80°的值。
答 案：
4、已知等差数列前n项和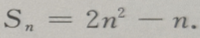
（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和
答 案：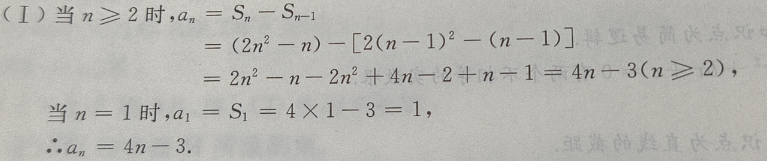
填空题
1、在自然数1、2、…、100中任取一个数，该数能被3整除的概率是______。
答 案：0.33
解 析：此题随机试验包含的基本事件总数n=100，且每个数能被取到的机会均等，即属于等可能事件的概率能被3整除的自然数的个数m=33，故所求概率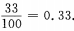
2、函数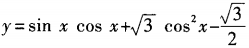
（x∈R）的最小值为______。
答 案：-1
解 析：
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
