2024年成考高起点《数学(文史)》每日一练试题12月08日
2024-12-08 12:34:15 来源:吉格考试网
2024年成考高起点《数学(文史)》每日一练试题12月08日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设集合S={(x,y)|xy>0},T={(x,y)|x>0,且y>0},则
- A:S∪T=S
- B:S∪T=T
- C:S∩T=S
- D:S∩T=∅
答 案:A
解 析:由已知条件可知集合S表示的是第第一,三象限的点集,集合T表示的是第一象限内点的集合,所以 所以有S∪T=S,S∩T=T,所以选择A。
所以有S∪T=S,S∩T=T,所以选择A。
2、若集合M={(x,y)|3x-2y=-1},N={(x,y)|2x+3y=8},则M∩N=()。
- A:(1,2)
- B:{1,2}
- C:{(1,2)}
- D:φ
答 案:C
解 析:M,N都是点集,所以只能选C。
3、已知向量i,j为互相垂直的单位向量,向量a=2i+mj,若|a|=2,则m=()
- A:-2
- B:-1
- C:0
- D:1
答 案:C
解 析:由题可知a=(2,m),因此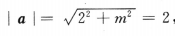 ,故m=0.
,故m=0.
4、函数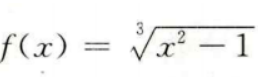 的定义域为()。
的定义域为()。
- A:R
- B:{1}
- C:{x||x|≤1}
- D:{x||xl≥1}
答 案:A
解 析:本题主要考查的知识点为函数的定义域。 对于 奇次根号下无要求,故函数的定义域为R。
奇次根号下无要求,故函数的定义域为R。
主观题
1、求证:双曲线的一个焦点到一条渐近线的距离等于虚半轴的长.
答 案:设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为
则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为 令设焦点F2(c,0)到渐近线
令设焦点F2(c,0)到渐近线 的距离为d,则
的距离为d,则 即从双曲线
即从双曲线 的一个焦点F2(c,0)到一条渐近线
的一个焦点F2(c,0)到一条渐近线 的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线
的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线 以及点F1(-c,0)到渐近线
以及点F1(-c,0)到渐近线 的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
解 析:本题考查的是圆锥曲线与直线位置关系的推理能力,主要是用代数的方法表示几何中的问题.考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解,方可解决此类综合题.这种综合性的圆锥曲线试题出现的概率比较高,要引起重视.
2、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。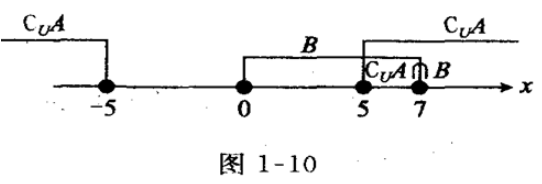
3、弹簧的身长与下面所挂砝码的重量成正比,知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm,写出弹簧长度y(cm)与砝码重x(g)的函数关系式,并求弹簧不挂砝码时的长度
答 案:设弹簧原长为y0cm,则弹簧伸长量为(y-y0)cm。 由题意得 y-y0 =kx,即 y= kx+y0, 所求函数关系式为y=0.2x+8,弹簧的原长为8CM
所求函数关系式为y=0.2x+8,弹簧的原长为8CM
4、设椭圆的中心是坐标原点,长袖在x轴上,离心率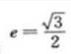 ,已知点P(0,3/2)到椭圆上的点的最远距离是
,已知点P(0,3/2)到椭圆上的点的最远距离是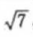 ,求椭圆的方程。
,求椭圆的方程。
答 案:
填空题
1、函数y=-x²+ax图像的对称轴为x=2,则a=______。
答 案:4
解 析:本题主要考查的知识点为二次函数的性质。 由题意,该函数图像的对称轴为 得a=4。
得a=4。
2、“a=0,且b=0”是“a2+b2=0的”______。
答 案:充要条件
2024年成考高起点《数学(文史)》每日一练试题08月12日 08-12 2023年成考高起点《数学(文史)》每日一练试题08月12日 08-12 2023年成考高起点《数学(文史)》每日一练试题12月08日 12-08 2022年成考高起点《数学(文史)》每日一练试题08月12日 08-12 2022年成考高起点《数学(文史)》每日一练试题12月08日 12-08 2024年成考高起点《数学(文史)》每日一练试题12月12日 12-12 2024年成考高起点《数学(文史)》每日一练试题08月08日 08-08 2023年成考高起点《数学(文史)》每日一练试题12月12日 12-12



