2024年成考高起点《数学(文史)》每日一练试题12月07日
2024-12-07 12:16:55 来源:吉格考试网
2024年成考高起点《数学(文史)》每日一练试题12月07日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设甲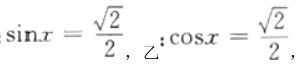 则()。
则()。
- A:甲是乙的充分条件但不是必要条件
- B:甲是乙的必要条件但不是充分条件
- C:甲是乙的充要条件
- D:甲既不是乙的充分条件也不是乙的必要条件
答 案:D
解 析:本题主要考查的知识点为简易逻辑. 由于,故甲既不是乙的充分条件,也不是乙的必要条件
2、一批产品共有5件,其中4件为正品,1件为次品,从中一次取出2件均为正品的概率为()。
- A:0.6
- B:0.5
- C:0.4
- D:0.3
答 案:A
解 析:本题主要考查的知识点为随机事件的概率。 一次取出2件均为正品的概率为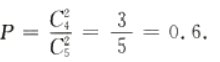
3、
- A:(-∞,-6)∪(1,+∞)
- B:(-6,1)
- C:(-∞,2)∪(3,+∞)
- D:(2,3)
答 案:B
解 析: 求必须有6-5x-x2>0,即x2+5x-6<0,即(x+6)(x-1)<0,解得-6
求必须有6-5x-x2>0,即x2+5x-6<0,即(x+6)(x-1)<0,解得-6
4、一射击手独立射击8次,每次中靶的概率是0.7,那么恰好中靶5次的概率是()。
- A:
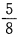
- B:
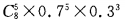
- C:
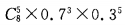
- D:
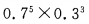
答 案:B
解 析:此题试验属于独立重复试验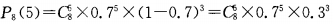 ,故应选B。
,故应选B。
主观题
1、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。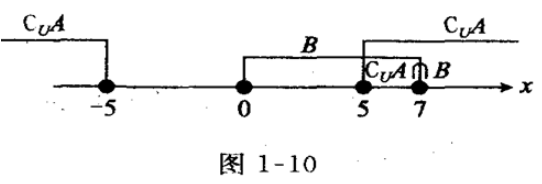
2、已知lg2=a,lg3=b,求lg0.15关于a,b的表达式。
答 案: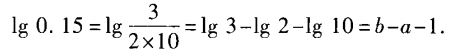
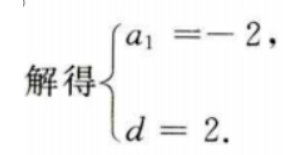
3、已知等差数列{an}中,a1+a3+a5=6,a2+a4+a6=12,求{an}的首项与公差.
答 案:因为{an}为等差数列,则
4、教室里有50人在开会,其中学生35人,家长12人,老师3人,现校长在门外听到有人在发言,那么发言人是老师或学生的概率为多少?
答 案:此题属于互斥事件,发言人是老师的概率为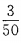 ,是学生的概率为
,是学生的概率为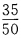 ,故所求概率为。
,故所求概率为。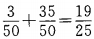
填空题
1、已知点P(-3,1)为角α终边上一点,则cos(2α-π)的值等于______。
答 案: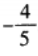
解 析:因为cos(2α-π)=cos(π-2α)=-cos2α。由已知,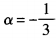 所以
所以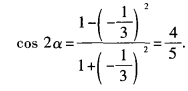
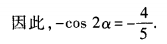
2、已知10x=3,10y=4,则103(x-y)的值等于______。
答 案: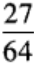
解 析:由已知,103x=27,103y=64,原式=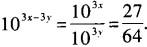
2024年成考高起点《数学(文史)》每日一练试题07月12日 07-12 2023年成考高起点《数学(文史)》每日一练试题07月12日 07-12 2023年成考高起点《数学(文史)》每日一练试题12月07日 12-07 2022年成考高起点《数学(文史)》每日一练试题07月12日 07-12 2022年成考高起点《数学(文史)》每日一练试题12月07日 12-07 2024年成考高起点《数学(文史)》每日一练试题12月12日 12-12 2024年成考高起点《数学(文史)》每日一练试题07月07日 07-07 2023年成考高起点《数学(文史)》每日一练试题12月12日 12-12



